[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Tìm giao điểm, giao tuyến, thiết diện trong hình học không gian
Ở topic này, mình sẽ không nhắc lại lí thuyết nữa, nên các bạn tự xem ở đây nhé Tổng hợp kiến thức toán 11 ; Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Mình sẽ hướng dẫn từng ví dụ cụ thể cho những bạn mới học hình không gian, hoặc học một thời gian mà vẫn chưa định hướng được cách làm nhé
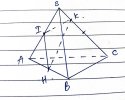
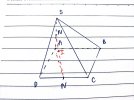
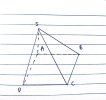
VD1: Cho mặt phẳng [imath](\alpha)[/imath] có các cặp cạnh đối không song song. Một điểm [imath]S \notin (\alpha)[/imath].
a) Xác định giao tuyến của [imath](SAC)[/imath] và [imath](SBD)[/imath]
b) Xác định giao tuyến của [imath](SAB)[/imath] và [imath](SCD)[/imath]
c) Xác định giao tuyến của [imath](SAD)[/imath] và [imath](SBC)[/imath]
a) Hai mặt phẳng này có 1 điểm chung là [imath]S[/imath]
Vậy ta cần tìm thêm điểm chung thứ 2
Xét xem các cặp đường nào có thể giao nhau
Do [imath]ABCD[/imath] không có các cặp cạnh nào song song nên các đường sẽ giao nhau
Gọi [imath]O = AC \cap BD[/imath]
Vậy [imath](SAC) \cap (SBD) = SO[/imath]
b) Tương tự: [imath]AB \cap CD = K[/imath]
Giao tuyến là [imath]SK[/imath]
c) Các bạn đọc tự làm nhé !
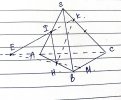
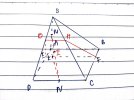
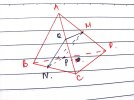
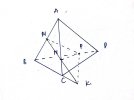
VD2: Cho hình chóp [imath]S.ABCD[/imath]. Gọi M là trung điểm của [imath]SB[/imath] ; [imath]N[/imath] là trung điểm của [imath]SD[/imath]. Tìm thiết diện của hình chóp cắt bởi mặt phẳng [imath](AMN)[/imath]

Định hướng:
mp [imath](AMN) \cap SA = A; (AMN) \cap SB =M ; (AMN) \cap SD = N[/imath]
Vậy ta cần tìm [imath](AMN) \cap SC = I[/imath]
Giả sử gọi [imath]K[/imath] là giao điểm của [imath]AM[/imath] và [imath](SCD)[/imath]. Khi đó: [imath]K;N \in (SCD)[/imath] nên sẽ cắt được [imath]SC[/imath] và đó cũng chính là giao điểm của [imath](AMN)[/imath] và [imath]SC[/imath]
Hướng đi cụ thể:
Tìm giao tuyến của [imath](SAB)[/imath] và [imath](SCD)[/imath] : [imath]AB \cap CD = O[/imath]
2 mp này có 2 điểm chung là [imath]O; S[/imath]. Nên giao tuyến chung : [imath](SAB) \cap (SCD) = SO[/imath]
Tìm giao điểm của [imath]AM[/imath] và [imath](SCD)[/imath]( Tìm xem [imath]AM[/imath] sẽ cắt đường nào trong mp[imath](SCD)[/imath])
Đường đó chính là [imath]SO[/imath]. Vì [imath]SO \in (SAB)[/imath]. Tìm được điểm [imath]K[/imath]
[imath]KN \cap SC = I[/imath]. Ta có: [imath]I \in KN[/imath] mà [imath]K \in (AMN) ; N \in (AMN)[/imath] nên [imath]I \in (AMN)[/imath]
Suy ra: [imath](AMN) \cap SC =I[/imath]
Thiết diện cần tìm là: [imath]AMIN[/imath]
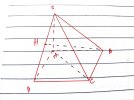
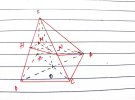
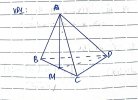
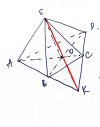
VD3: Cho 4 điểm [imath]A;B;C;D[/imath] không cùng thuộc một mặt phẳng. Trên các đoạn thẳng [imath]AB ; AC;BD[/imath] lần lượt lấy các điểm [imath]M;N;P[/imath] sao cho [imath]MN[/imath] không song song với [imath]BC[/imath]. Tìm giao tuyến của [imath](BCD)[/imath] và [imath](MNP)[/imath]

Ta có: [imath]P \in BD[/imath] nên [imath]P \in (BCD)[/imath]
Nên 2 mặt phẳng này có 1 điểm chung là [imath]P[/imath]
Cần tìm điểm chung thứ 2
Xét xem có một đường nào đó thuộc mặt phẳng [imath](MNP)[/imath] sẽ cắt [imath](BCD)[/imath]
Thì ta có ngay [imath]MN \cap CD[/imath] ( [imath]MN[/imath] không song song [imath]BC[/imath] như bài toán đã cho)
[imath]MN \cap CD = K[/imath]
Ta có: [imath]K \in MN[/imath] nên [imath]K \in (MNP)[/imath]
[imath]K \in BC[/imath] nên [imath]K \in (BCD)[/imath]
Suy ra: [imath]K = (BCD) \cap (MNP)[/imath]
Vậy giao tuyến là [imath]PK[/imath]
Chờ đợi tiếp các bài tiếp theo trong tuần sau nhé hihi
Last edited: