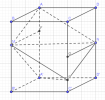
Chị nghĩ đề cho cạnh hình thoi bằng a á, em coi lại đề nha, kh cho thì kh tìm được góc
[imath](ABB'A')//(CDD'C'); (AMN)\cap(ABB'A')=AM; (AMN)\cap (CDD'C')={NP}\Rightarrow AM//NP[/imath]
Kẻ [imath]NG//CD[/imath]
[imath]\Rightarrow \Delta AMF=\Delta PNG[/imath] (cgc)
[imath]\Rightarrow GP=AF=BM=\dfrac13BB'[/imath]
[imath]\Rightarrow CP=CG+GP=\dfrac56BB'[/imath]
[imath]\overrightarrow{AB}.\overrightarrow{AD}=AB.AD.\cos(AD,AB)=a^2.(-\cos \alpha)[/imath]
[imath]\overrightarrow{AN}=\overrightarrow{AD}+\overrightarrow{DN}=\overrightarrow{AD}+\dfrac12\overrightarrow{AA'}[/imath]
[imath]\Rightarrow AN=a\dfrac{\sqrt5}{2}[/imath]
[imath]\overrightarrow{A'P}=\overrightarrow{A'C'}+\overrightarrow{C'P}=\overrightarrow{AB}+\overrightarrow{AD}-\dfrac16\overrightarrow{AA'}[/imath]
[imath]\Rightarrow A'P=a\sqrt{\dfrac{73}{36}-2\cos \alpha}[/imath]
[imath]\overrightarrow{AN}.\overrightarrow{A'P}=a^2(-\cos \alpha+\dfrac{11}{12})[/imath]
[imath]\cos (A'P,AN)=\dfrac{\overrightarrow{AN}.\overrightarrow{AP}}{AN.A'P}=\dfrac{1}{\sqrt2}[/imath]
[imath]a\dfrac{\sqrt{10}}{2}.a\sqrt{\dfrac{73}{36}+2\cos \alpha}=a^2(-\cos \alpha+\dfrac{11}{12})[/imath]
[imath]\Rightarrow \dfrac{5}8\left(\dfrac{73}{36}-2\cos \alpha\right)=\cos \alpha^2-\dfrac{11}6\cos \alpha+\dfrac{121}{144}[/imath]
[imath]\Rightarrow \left\{\begin{matrix}x=\dfrac{7+\sqrt{295}}{24}(l)\\x=\dfrac{7-\sqrt{295}}{24} (n)\end{matrix}\right.[/imath]
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em tham khảo thêm tại
Hệ thống bài tập trắc nghiệm đường thẳng vuông góc với mặt phẳng
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.