[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
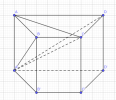
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang cân,. AD song song với BC, AB=BC=CD=a, AD= 2a. Góc giữa hai mặt phẳng (A'CD) và (ABCD) bằng 45 độ (em tìm được là góc A'CA)
1. Tính khoảng cách từ B đến mặt phẳng (A'CD)
em đã tính được và bằng [math]\frac{a\sqrt{6}}{4}[/math]2. Tính cos của góc giữa hai mặt phẳng (A'BC) và (A'CD)
Em nghĩ là sẽ dùng
sin ((A'BC),(A'CD))= [math]\frac{d(B,(A'CD))}{d(B,A'C)}[/math]Em cần mn giúp tính d(B,A'C) ạ. Hoặc làm theo cách khác ạ.
Em cảm ơn nhiều.
1. Tính khoảng cách từ B đến mặt phẳng (A'CD)
em đã tính được và bằng [math]\frac{a\sqrt{6}}{4}[/math]2. Tính cos của góc giữa hai mặt phẳng (A'BC) và (A'CD)
Em nghĩ là sẽ dùng
sin ((A'BC),(A'CD))= [math]\frac{d(B,(A'CD))}{d(B,A'C)}[/math]Em cần mn giúp tính d(B,A'C) ạ. Hoặc làm theo cách khác ạ.
Em cảm ơn nhiều.