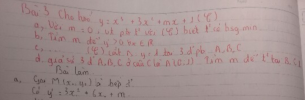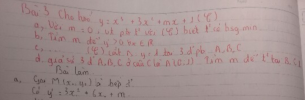Cho hàm số [imath]y=x^{3} +3x^{2} +mx+1[/imath] ([imath]C[/imath])
c, Tìm m để ([imath]C[/imath]) cắt [imath]\Delta: y=1[/imath] tại 3 điểm phân biệt A, B, C
d, Giả sử 3 điểm A ở câu c là [imath]A(0;1)[/imath]; tìm m để tiếp tuyến tại B và C vuông góc với nhau
View attachment 211464
em còn câu c, d không làm đc; mng giúp em với ạ
Bảo Linh _Vũc) Phương trình hoành độ giao điểm: [imath]x^3+3x^2+mx+1=1 \Leftrightarrow x(x^2+3x+m)=0 \Leftrightarrow \left[\begin{array}{l} x=0 \\ x^2+3x+m=0 \end{array}\right.[/imath]
Để phương trình trên có [imath]3[/imath] nghiệm phân biệt thì [imath]\begin{cases} m \neq 0 \\ \Delta =3^2-4m=9-4m \geq 0 \end{cases} \Leftrightarrow \begin{cases} m \neq 0 \\ m \leq \dfrac{9}{4} \end{cases}[/imath]
d) Xét tọa độ điểm [imath]B=(x_1,1),C(x_2,1)[/imath]. Khi đó [imath]x_1,x_2[/imath] là nghiệm của [imath]x^2+3x+m=0[/imath].
Áp dụng định lý Vi-ét ta có [imath]\begin{cases} x_1+x_2=-3 \\ x_1x_2=m \end{cases}[/imath]
Đặt [imath]y=f(x)=x^3+3x^2+mx+1[/imath] thì [imath]f'(x)=3x^2+6x+m[/imath]
Hệ số góc của tiếp tuyến tại [imath]B[/imath] là [imath]f'(x_1)=3x_1^2+6x_1+m=3(x_1^2+3x_1+m)-3x_1-2m=-3x_1-2m[/imath]
Hệ số góc tiếp tuyến tại [imath]C[/imath] là [imath]f'(x_2)=3x_2^2+6x_2+m=-3x_2-2m[/imath]
Để tiếp tuyến của [imath]B,C[/imath] vuông góc với nhau thì tích hệ số góc của 2 đường thẳng bằng [imath]-1[/imath], tức:
[imath](-3x_1-2m)(-3x_2-2m)=-1 \Leftrightarrow 9x_1x_2+6m(x_1+x_2)+4m^2=-1[/imath]
[imath]\Leftrightarrow 9m+6m(-3)+4m^2=-1[/imath]
[imath]\Leftrightarrow 4m^2-9m+1=0 \Leftrightarrow m=\dfrac{9 \pm \sqrt{65}}{8}[/imath]
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
Bài toán liên quan về tiếp tuyến
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.