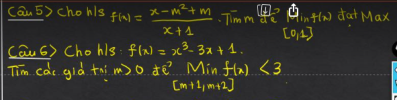- 5 Tháng mười hai 2018
- 441
- 187
- 86
- Hà Tĩnh
- Tuấn Thiện
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
5. Cho hàm số [imath]f(x)=\dfrac{x-m^2+m}{x+1}[/imath]. Tìm [imath]m[/imath] để [imath]\min _{[0,1]} f(x)[/imath] đạt [imath]\max[/imath]
6. Cho hàm số [imath]f(x)=x^3-3x+1[/imath]. Tìm các giá trị của [imath]m >0[/imath] để [imath]\min _{[m+1,m+2]} f(x) < 3[/imath]
Làm giùm mình câu 5 và câu 6 với ạ. Mình cảm ơn
6. Cho hàm số [imath]f(x)=x^3-3x+1[/imath]. Tìm các giá trị của [imath]m >0[/imath] để [imath]\min _{[m+1,m+2]} f(x) < 3[/imath]
Làm giùm mình câu 5 và câu 6 với ạ. Mình cảm ơn
Attachments
Last edited by a moderator: