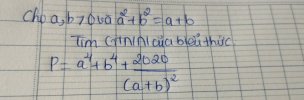Đặt [imath]t=a+b >0[/imath]
Áp dụng hệ quả bất đẳng thức [imath]A-G[/imath] ta có: [imath]a^2+b^2 \geq \dfrac{(a+b)^2}{2} \Rightarrow 2t \geq t^2 \Rightarrow t \leq 2[/imath]
Áp dụng hệ quả bất đẳng thức [imath]A-G[/imath] ta có: [imath]a^4+b^4 \geq \dfrac{(a^2+b^2)^2}{2} = \dfrac{t^2}{2}[/imath]
[imath]\Rightarrow P \geq \dfrac{t^2}{2} + \dfrac{2020}{t^2}[/imath]
Áp dụng bất đẳng thức [imath]A-G[/imath] ta có: [imath]\dfrac{t^2}{2} + \dfrac{8}{t^2} \geq 4[/imath]
Mà [imath]t \leq 2 \Rightarrow t^2 \leq 4 \Rightarrow \dfrac{2012}{t^2} \geq 503[/imath]
Từ đó suy ra [imath]P \geq 507[/imath]
Dấu = xảy ra khi [imath]a=b=1[/imath]
Chúc may mắn, ngoài ra mời e ghé qua topic: [Lý thuyết] Chuyên đề HSG : Bất đẳng thức
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.