[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
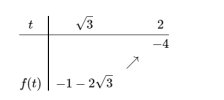
[imath]x^2-2\sqrt{x^2-2x+4}\le 2x-a[/imath]
[imath]\Leftrightarrow x^2-2x+4-2\sqrt{x^2-2x+4}-4 \le -a[/imath]
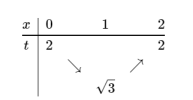
Đặt [imath]t=\sqrt{x^2-2x+4}[/imath]
View attachment 207698
Dựa vào bbt ta có: [imath]t\in [3,4][/imath]
bpt trở thành [imath]t^2-2t-4\le -a[/imath]
Xét [imath]f(t)=t^2-2t-4[/imath]
View attachment 207699
[imath]f(t)\le -a \forall t\in [3,4]\Leftrightarrow -a\ge 4\Leftrightarrow a\le -4[/imath]
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em tham khảo thêm tại Tổng hợp kiến thức Hình học cơ bản lớp 10 | Đại số cơ bản lớp 10
chị quên dấu căn ở bbt 1, xin lỗi em nha, em xem lại bài chị đã sửa nhé
chị ơi, tại sao lại chọn nghiệm 2 ạ?
f(t)≤−a∀t∈[3,2]⇔−a≥−4⇔a≤4
View attachment 207706
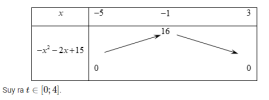
Bài này ko liên quan nhưng chị giải thích giúp em chỗ t với ạ, em tưởng t ∈[0,16] chứ ạ?
em cảm ơn ạ:>
[imath]-a\ge f(t) \forall t\in [\sqrt3,2][/imath]
thì [imath]-a[/imath] phải [imath]\ge[/imath] GTLN của [imath]f(t)[/imath] trên [imath][\sqrt3,2][/imath]
GTLN của [imath]f(t)[/imath] trên [imath][\sqrt3,2][/imath] là [imath]f(2)[/imath]
câu dưới thì em xem lại người ta đặt t là gì nhé, chị nghĩ là [imath]t=\sqrt{-x^2-2x+15}[/imath] í