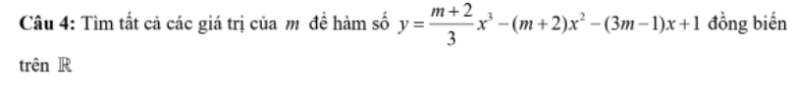Ta xét [imath]m=-2[/imath] lúc này hàm số trở thành [imath]y = 7x + 1 \to[/imath] hàm số đồng biến trên [imath]R[/imath] => chọn ([imath]1[/imath])
Ta xét [imath]m[/imath] khác -2 ta có [imath]y' = (m+2).x^2 -2.(m+2)x -3m +1[/imath]
Để hàm số đồng biến trên [imath]R[/imath] thì [imath]y' \ge 0[/imath] với mọi [imath]x[/imath] thuộc [imath]R[/imath]
[imath]\to \Delta ' \le 0[/imath] và [imath](m+2) > 0[/imath]
Tức là [imath](m+2)^2 - (-3m+1).(m+2) = 4m^2 + 9m +2 \le 0[/imath] và [imath]m>-2[/imath]
[imath]\to -2\le m\le-\dfrac{1}{4}[/imath] và [imath]m>-2[/imath]
Kết hợp hai điều kiên trên ta được [imath]-2 < m -\dfrac{1}{4}[/imath] ([imath]2[/imath])
Từ ([imath]1[/imath]) và ([imath]2[/imath]) ta được [imath]-2\le m\le-\dfrac{1}{4}[/imath]
Có gì không hiểu thì bạn hỏi lại nha
Tham khảo thêm kiến thức tại
đây.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.