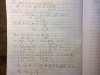Toán 9 Tìm giá trị của m để...

[Ngoc Anhs]

Sao mình lại giải ra khác nhỉ ???
\[m{{x}^{2}}-(m+1)x+3-2m=0\]
Pt có 2 nghiệm khi \[m\ne 0\]
Khi đó pt là pt bậc 2
\[\begin{align}
& \vartriangle ={{(m+1)}^{2}}-4m(3-2m)={{m}^{2}}+2m+1-12m+8{{m}^{2}}=9{{m}^{2}}-10m+1\ge 0 \\
& \Rightarrow x\ge 1;x\le \frac{1}{9} \\
\end{align}\]
\[\begin{align}
& Viet:{{x}_{1}}+{{x}_{2}}=\frac{m+1}{m};{{x}_{1}}.{{x}_{2}}=\frac{3-2m}{m} \\
& {{x}_{1}},{{x}_{2}}\ne 0\Rightarrow {{x}_{1}}.{{x}_{2}}=\frac{3-2m}{m}\ne 0\Rightarrow m\ne \frac{3}{2} \\
& \frac{1}{{{x}_{1}}}+\frac{1}{{{x}_{2}}}>2 \\
& \frac{{{x}_{1}}+{{x}_{2}}}{{{x}_{1}}.{{x}_{2}}}>2 \\
& \frac{m+1}{3-2m}-2>0 \\
& \frac{5m-5}{3-2m}>0 \\
& \frac{m-1}{2m-3}<0 \\
& \frac{2m-2}{2m-3}<0 \\
& \Rightarrow 2m-2>0;2m-3<0\Rightarrow 1<m<\frac{3}{2} \\
\end{align}\]
Vậy \[1<m<\frac{3}{2}\]

Hihi... Em nhầm... Nãy giờ mải tranh luận đk m khác 0 mà quên luôn kết quả

Sao mình lại giải ra khác nhỉ ???
\[m{{x}^{2}}-(m+1)x+3-2m=0\]
Pt có 2 nghiệm khi \[m\ne 0\]
Khi đó pt là pt bậc 2
\[\begin{align}
& \vartriangle ={{(m+1)}^{2}}-4m(3-2m)={{m}^{2}}+2m+1-12m+8{{m}^{2}}=9{{m}^{2}}-10m+1\ge 0 \\
& \Rightarrow x\ge 1;x\le \frac{1}{9} \\
\end{align}\]
\[\begin{align}
& Viet:{{x}_{1}}+{{x}_{2}}=\frac{m+1}{m};{{x}_{1}}.{{x}_{2}}=\frac{3-2m}{m} \\
& {{x}_{1}},{{x}_{2}}\ne 0\Rightarrow {{x}_{1}}.{{x}_{2}}=\frac{3-2m}{m}\ne 0\Rightarrow m\ne \frac{3}{2} \\
& \frac{1}{{{x}_{1}}}+\frac{1}{{{x}_{2}}}>2 \\
& \frac{{{x}_{1}}+{{x}_{2}}}{{{x}_{1}}.{{x}_{2}}}>2 \\
& \frac{m+1}{3-2m}-2>0 \\
& \frac{5m-5}{3-2m}>0 \\
& \frac{m-1}{2m-3}<0 \\
& \frac{2m-2}{2m-3}<0 \\
& \Rightarrow 2m-2>0;2m-3<0\Rightarrow 1<m<\frac{3}{2} \\
\end{align}\]
Vậy \[1<m<\frac{3}{2}\]

Ơ mà có gì đó sai sai nha!
Phần ∆ lớn hơn bằng 0 thì phải là đk của m chứ sao lại là x

 

[Sơn Nguyên 05]

1) Tìm giá trị của m để [tex]f(x) = x^{2} - 2mx + 4 > 0[/tex]
2) Cho phương trình [tex]mx^{2} - (m+1)x + 3 - 2m = 0[/tex]. Khi phương trình có hai nghiệm x1, x2, tìm giá trị của m để [tex]\frac{1}{x_{1}} + \frac{1}{x_{2}} > 2[/tex]

Tham khảo câu 2.