hieult
[imath]a/[/imath]
- Vạch thứ nhất của dãy Laiman ứng với electron chuyển từ quỹ đạo dừng [imath]n=2[/imath] về [imath]n=1[/imath]:
[imath]\dfrac{hc}{\lambda }=E_2-E_1 \ (1 )[/imath]
- Vạch [imath]H_{\alpha}[/imath] của dãy Banme ứng với electron chuyển từ quỹ đạo dừng [imath]n=3[/imath] về [imath]n=2[/imath]:
[imath]\dfrac{hc}{\lambda_\alpha }=E_3-E_2 \ (2 )[/imath]
- Vạch đầu tiên của dãy Pasen ứng với electron chuyển từ quỹ đạo dừng [imath]n=4[/imath] về [imath]n=3[/imath]:
[imath]\dfrac{hc}{\lambda_{1} }=E_4-E_3 \ (3 )[/imath]
- Vạch thứ ba của dãy Laiman ứng với electron chuyển từ quỹ đạo dừng [imath]n=4[/imath] về [imath]n=1[/imath]:
[imath]\dfrac{hc}{\lambda_{3} }=E_4-E_1 \ (4)[/imath]
- Lấy [imath](3)[/imath] cộng [imath](2)[/imath] vế theo vế được:
[imath]hc. (\dfrac{1}{\lambda_{1}}+\dfrac{1}{\lambda _\alpha })=E_4-E_2 \ (5)[/imath]
- Lấy [imath](5)[/imath] cộng [imath](1)[/imath] vế theo vế được:
[imath]hc. (\dfrac{1}{\lambda_{1}}+\dfrac{1}{\lambda _\alpha }+\dfrac{1}{\lambda })=E_4-E_1 \ (6)[/imath]
- Thay [imath](6)[/imath] vào [imath](4)[/imath] được:
[imath]\dfrac{1}{\lambda _3}=\dfrac{1}{\lambda_{1}}+\dfrac{1}{\lambda _\alpha }+\dfrac{1}{\lambda }\Rightarrow \lambda _3\approx 0,097 \mu m[/imath] | 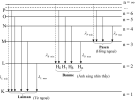 |
[imath]b/[/imath]
Các quỹ đạo ta đang xét là [imath]K,L,M,N[/imath]
Mình tính mẫu vận tốc trên quỹ đạo [imath]K[/imath] thôi nhé, [imath]3[/imath] quỹ đạo còn lại chỉ việc thay số thôi.
- Tinh vận tốc trên quỹ đạo [imath]K[/imath]:
Bán kính quỹ đạo: [imath]r_1=r_0.1^2=5,3.10^{-11}m[/imath]
Lực điện đóng vai trò là lực hướng tâm nên:
[imath]F_đ = F_{ht} \hArr \dfrac{9.10^9 . e^2}{r_1^2}=\dfrac{m.v_K^2}{r_1} \Rightarrow v_K = \sqrt[]{\dfrac{9.10^9.e^2}{m.r_1}}=\sqrt{\dfrac{9.10^9. (1,6.10^{-19})^2}{9,1.10^{-31}.5,3.10^{-11}}}=2185660,011 \ m/s[/imath]
Chúc bạn học tốt!
-----
Xem thêm:
Tổng hợp những điều quan trọng trong chương Lượng tử ánh sáng
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.