[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 1: Quy tắc cộng và quy tắc nhân
I) Quy tắc cộng1) Định nghĩa
Giải sử một công việc có thể được thực hiện theo phương án A hoặc phương án B. Có [imath]n[/imath] cách thực hiện phương án A và [imath]m[/imath] cách thực hiện phương án B. Khi đó công việc được thực hiện theo [imath]m+n[/imath] cách
2) Công thức quy tắc cộng
Nếu các tập [imath]A_{1},A_{2},...,A_{n}[/imath] đôi một rời nhau. Khi đó:
[imath]\left | A_{1}\cup A_{2}\cup ...\cup A_{n} \right |=\left | A_{1} \right |+\left | A_{2} \right |+...+\left | A_{n} \right |[/imath] ( trong đó: [imath]\left | X \right |[/imath] là chỉ số phần tử của tập [imath]X[/imath])
VD1: Hà có 5 cuốn sách khoa họ, 4 cuốn tiểu thuyết và 3 cuốn truyện tranh (các cuốn sách khác nhau từng đôi một). Hà đồng ý cho Nam mượn một cuốn sách trong số đố để đọc. Nam có bao nhiêu cách chọn 1 cuốn sách để mượn?
Lời giải:
Phương án 1: Mượn một cuốn sách khoa học, có 5 cách
Phương án 2: Mượn 1 cuốn tiểu thuyết, có 4 cách
Phương án 3: Mượn 1 cuốn truyện tranh, có 3 cách
Vậy theo quy tắc cộng, Nam có [imath]5+4+3 = 12[/imath] cách chọn 1 cuốn sách để mượn
VD2: Một hộp có chứa 15 bóng đèn màu trắng và 10 bóng đèn màu xanh. Số cách chọn được một bóng đèn trong hộp đó là?
Lời giải:
Phương án 1: Chọn 1 bóng đèn màu trắng có: [imath]15[/imath] cách
Phương án 2: Chọn 1 bóng đèn màu xanh có [imath]10[/imath] cách
Vậy theo quy tắc cộng có [imath]15 + 10 = 25[/imath] cách chọn 1 bóng đèn trong hộp
VD3: Lớp 11 A1 có 18 học sinh nữ và 20 học sinh nam. Hỏi có bao nhiêu cách chọn một học sinh trong lớp làm lớp trưởng?
Lời giải:
Phương án 1: Chọn 1 bạn nữ làm lớp trưởng có: 18 cách
Phương án 2: Chọn 1 bạn nam làm lớp trưởng có 20 cách
Vậy theo quy tắc cộng, có: [imath]18+20 = 38[/imath] cách chọn 1 học sinh làm lớp trưởng
II) Quy tắc nhân
1) Định nghĩa
Giả sử một công việc nào đó bao gồm 2 công đoạn A và B. Công đoạn A có thể làm theo [imath]m[/imath] cách. Với mỗi cách thực hiện công đoạn A thì công đoạn B có thể thực hiện theo [imath]n[/imath] cách. Khi đó công việc có thể thực hiện theo [imath]m.n[/imath] cách
2) Công thức quy tắc nhân
Nếu các tập [imath]A_{1},A_{2},..,A_{n}[/imath] đôi một rời nhau. Khi đó: [imath]\left | A_{1}\cap A_{2}\cap ...\cap A_{n} \right |=\left | A_{1} \right |.\left | A_{2} \right |....\left | A_{n} \right |[/imath]
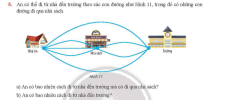
VD1: Từ A đến B có 3 con đường, từ B đến C có 5 con đường. Hỏi có bao nhiêu cách chọn đường từ A đến C (qua B)?
Lời giải:
Công đoạn 1: Đi từ A đến B có 3 cách
Công đoạn 2: Đi từ B đến C có 5 cách
Vậy theo quy tắc nhân, có [imath]3.5 = 15[/imath] cách đi từ A đến C
VD2: Từ 5 chữ số [imath]1; 2; 3; 4;5[/imath]. Lập được bao nhiêu số có 5 chữ số khác nhau?
Lời giải:
Gọi số cần lập là [imath]\overline{abcd}[/imath]
Công đoạn 1: Có 5 cách chọn chữ số [imath]a[/imath]
Công đoạn 2: Có 4 cách chọn chữ số [imath]b[/imath]
Công đoạn 3: Có 3 cách chọn chữ số [imath]c[/imath]
Công đoạn 4: Có 2 cách chọn chữ số [imath]d[/imath]
Công đoạn 5: Có 1 cách chọn chữ số [imath]e[/imath]
Vậy theo quy tắc nhân, lập được: [imath]5.4.3.2.1 = 120[/imath] số
VD3: Bạn An đang cần chọn một bộ quần áo và cà vạt để đi dự tiệc. Biết rằng An có 8 chiếc quần; 5 chiếc áo và 5 cái cà- vạt .Hỏi An có bao nhiêu cách chọn?
Lời giải:
Công đoạn 1: Chọn Áo có 5 cách
Công đoạn 2: Chọn quần có 8 cách
Công đoạn 3: Chọn cà vạt có 5 cách
Vậy theo quy tắc nhận có: [imath]5.8.5 = 200[/imath] cách chọn
Last edited: