[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
TÍCH CỦA MỘT VECTƠ VỚI MỘT SỐ
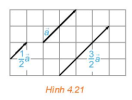
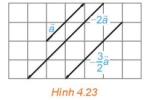
1. Tích của một vectơ với một sốTích của một vectơ [imath]\overrightarrow{a}\ne \overrightarrow{0}[/imath] với một số thực [imath]k>0[/imath] là một vectơ, kí hiệu [imath]k\overrightarrow{a}[/imath], cùng hướng với vectơ [imath]\overrightarrow{a}[/imath] và có độ dài bằng [imath]k|\overrightarrow{a}|[/imath]
Tích của một vectơ [imath]\overrightarrow{a}\ne \overrightarrow{0}[/imath] với một số thực [imath]k<0[/imath] là một vectơ, kí hiệu [imath]k\overrightarrow{a}[/imath], ngược hướng với vectơ [imath]\overrightarrow{a}[/imath] và có độ dài bằng [imath](-k)|\overrightarrow{a}|[/imath]
Ví dụ: Trong [imath]\Delta ABC[/imath], hai trung tuyến AM và BN của tam giác ABC cắt nhau tại G.
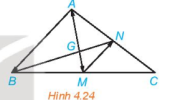
Ta có: [imath]\overrightarrow{GA}=-2\overrightarrow{GM}, \overrightarrow{MN}=\dfrac{-1}2\overrightarrow{AB}[/imath]
Luyện tập 1. Cho đường thẳng d đi qua hai điểm phân biệt A và B. Những khẳng định nào sau đây là đúng?
a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để [imath]\overrightarrow{AM}=t\overrightarrow{AB}[/imath]
[imath](\Rightarrow )[/imath] M thuộc đường thẳng d
Khi đó tồn tại [imath]t=\dfrac{|\overrightarrow{AM}|}{|\overrightarrow{AB}|}[/imath] nếu M nằm bên phải A hoặc [imath]t=-\dfrac{|\overrightarrow{AM}|}{|\overrightarrow{AB}|}[/imath] nếu M nằm bên trái A
Do đó [imath]\overrightarrow{AM}=t\overrightarrow{AB}[/imath] (vì cùng độ dài và cùng hướng)
[imath](\Leftarrow)[/imath] Ta có: [imath]\overrightarrow{AM}=t\overrightarrow{AB}[/imath] nên [imath]\overrightarrow{AM},\overrightarrow{AB}[/imath] cùng phương với nhau, do đó [imath]AM//AB\Rightarrow A,M,B[/imath] thẳng hàng hay [imath]M\in d[/imath]
Vậy câu a) đúng
b) Với điểm M bất kì, ta luôn có [imath]\overrightarrow{AM}=\dfrac{AM}{AB}\overrightarrow{AB}[/imath]
Không đúng vì nếu M nằm khác phía với B so với A thì [imath]\overrightarrow{AM}=-\dfrac{AM}{AB}\overrightarrow{AB}[/imath]
c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số [imath]t\le 0[/imath] để [imath]\overrightarrow{AM}=t\overrightarrow{AB}[/imath] (đúng)
2. Các tính chất của phép nhân với một số
Với hai vectơ [imath]\overrightarrow{a},\overrightarrow{b}[/imath] và hai số thực [imath]k,t[/imath] ta luôn có:
[imath]k(t\overrightarrow{a})=(kt)\overrightarrow{a}[/imath]
[imath](k+t)\overrightarrow{a}=k\overrightarrow{a}+t\overrightarrow{a}[/imath]
[imath]k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{a}+k\overrightarrow{b}; k(\overrightarrow{a}-\overrightarrow{b})=k\overrightarrow{a}-k\overrightarrow{b}[/imath]
[imath]1\overrightarrow{a}=\overrightarrow{a}; (-1)\overrightarrow{a}=-\overrightarrow{a}[/imath]
Luyện tập 2. Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có
[math]\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}[/math]
Ta chứng minh [imath]\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}[/imath]
[imath]\iff \dfrac{2}3\overrightarrow{AD}+\dfrac{2}3\overrightarrow{BE}+\dfrac{2}3\overrightarrow{CF}=\overrightarrow{0}[/imath]
[imath]\iff \overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{BC}+\overrightarrow{CE}+\overrightarrow{CA}+\overrightarrow{AF}=\overrightarrow{0}[/imath]
[imath]\iff \dfrac{3}2\overrightarrow{AB}+\dfrac{3}2\overrightarrow{BC}+\dfrac{3}2\overrightarrow{CA}=\overrightarrow{0}[/imath]
[imath]\iff \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{0}[/imath] (luôn đúng)
Ta có: [imath]\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OG}-\overrightarrow{OA}+\overrightarrow{OG}-\overrightarrow{OB}+\overrightarrow{OG}-\overrightarrow{OC}=3\overrightarrow{OG}[/imath]
Chú ý: bài toán ở trên RẤT QUAN TRỌNG vì hay được xài, sau này được dùng luôn, không cần chứng minh lại.
