- 19 Tháng tám 2018
- 2,749
- 6,038
- 596
- 24
- Thái Bình
- Đại học Y Dược Thái Bình
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
TÍCH VÔ HƯỚNG CỦA HAI VECTOR
1. Góc giữa hai vectorCho hai vector [imath]\overrightarrow{u}[/imath] và [imath]\overrightarrow{v}[/imath] khác [imath]\overrightarrow{0}[/imath].
Từ một điểm [imath]A[/imath] tuỳ ý, vẽ các vector [imath]\overrightarrow{u} = \overrightarrow{AB}, \overrightarrow{v} = \overrightarrow{AC}[/imath].
Khi đó, số đo góc [imath]BAC[/imath] được gọi là số đo góc giữa hai vector [imath]\overrightarrow{u}[/imath] và [imath]\overrightarrow{v}[/imath] hay đơn giản là góc giữa vector [imath]\overrightarrow{u}, \overrightarrow{v}[/imath].
Kí hiệu là: [imath](\overrightarrow{u}, \overrightarrow{v})[/imath]
Chú ý:
- Quy ước giữa hai vector [imath]\overrightarrow{u}[/imath] và [imath]\overrightarrow{0}[/imath] có thể nhận một giá trị tuỳ ý từ [imath]0^\circ[/imath] đến [imath]180^\circ[/imath].
- Nếu [imath](\overrightarrow{u}, \overrightarrow{v}) = 90^\circ[/imath] thì ta nói rằng [imath]\overrightarrow{u}[/imath] và [imath]\overrightarrow{v}[/imath] vuông góc với nhau, kí hiệu là [imath]\overrightarrow{u} \perp \overrightarrow{v}[/imath] hoặc [imath]\overrightarrow{v} \perp \overrightarrow{u}[/imath]
- Đặc biệt [imath]\overrightarrow{0}[/imath] được coi là vuông góc với mọi vector
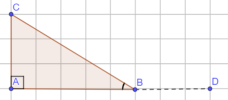
Giải:Ví dụ: Cho tam giác $ABC$ vuông tại $A$ và $\hat B = 30^\circ$. Tính $(\overrightarrow{AB}, \overrightarrow{AC}), (\overrightarrow{CA}, \overrightarrow{CB}), (\overrightarrow{AB}, \overrightarrow{BC})$
2. Tích vô hướng của 2 vector
Tích vô hướng của hai vector [imath]\overrightarrow{u}[/imath] và [imath]\overrightarrow{v}[/imath] là một số, kí hiệu là [imath]\overrightarrow{u}\cdot \overrightarrow{v}[/imath], được xác định bởi công thức sau: [imath]\overrightarrow{u}\cdot \overrightarrow{v} = |\overrightarrow{u}| \cdot |\overrightarrow{u}| \cdot \cos (\overrightarrow{u}, \overrightarrow{v})[/imath]
Chú ý:
- [imath]\overrightarrow{u} \perp \overrightarrow{v} \iff \overrightarrow{u}\cdot \overrightarrow{v} = 0[/imath]
- [imath]\overrightarrow{u}\cdot \overrightarrow{u}[/imath] còn được viết là [imath]\overrightarrow{u}^2[/imath] và được gọi là bình phương vô hướng của vector [imath]\overrightarrow u[/imath]. Ta có: [imath]\overrightarrow{u}^2 = |\overrightarrow{u}| \cdot |\overrightarrow{u}| \cdot \cos 0^\circ = |\overrightarrow{u}| ^2[/imath]
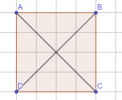
Ví dụ: Cho hình vuông $ABCD$ có cạnh bằng $a$. Tính các tích vô hướng sau: $\overrightarrow{AB} \cdot \overrightarrow{AD}, \overrightarrow{AB} \cdot \overrightarrow{AC}, \overrightarrow{AB} \cdot \overrightarrow{BD}$.
Giải:
3. Biểu thức toạ độ và tính chất của tích vô hướng
3.1 Định nghĩa
Tích vô hướng của hai vector [imath]\overrightarrow{u} = (x;y), \overrightarrow{v} = (x',y')[/imath] được tính theo công thức: [imath]\overrightarrow{u}\cdot \overrightarrow{v} = xx'+yy'[/imath]
Nhận xét:
- Hai vector [imath]\overrightarrow{u}[/imath] và [imath]\overrightarrow{v}[/imath] vuông góc với nhau khi và chỉ khi [imath]xx' + yy' = 0[/imath]
- Bình phương vô hướng của [imath]\overrightarrow{u} (x;y)[/imath] là: [imath]\overrightarrow{u}^2 = x^2 + y^2[/imath]
- Nếu [imath]\overrightarrow{u} \ne 0[/imath] và [imath]\overrightarrow{v} \ne 0[/imath] thì [imath]\cos (\overrightarrow{u}, \overrightarrow{u}) = \dfrac{\overrightarrow{u}\cdot \overrightarrow{v}}{|\overrightarrow{u}| \cdot |\overrightarrow{v}|} = \dfrac{xx' + yy'}{\sqrt{x^2 + y^2} \cdot \sqrt{x'^2 + y'^2}}[/imath]
Giải:Ví dụ: Trong mặt phẳng toạ độ $Oxy$, tính tích vô hướng của các cặp vector sau:
a. $\overrightarrow{u} = (2;-3), \overrightarrow{v} = (5;3)$.
b. Hai vector $\overrightarrow{i}, \overrightarrow{j}$ tương ứng với trục $Ox, Oy$.
a. Ta có: [imath]\overrightarrow{u}\cdot \overrightarrow{v} = 2 \cdot 5 + (-3) \cdot 3 = 1[/imath]
b. Vì [imath]\overrightarrow{i} = (1;0)[/imath] và [imath]\overrightarrow{j} = (0;1)[/imath] nên [imath]\overrightarrow{i}\cdot \overrightarrow{j} = 1 \cdot 0 + 0 \cdot 1 = 0[/imath]
3.2 Tích chất của tích vô hướng
Với ba vector [imath]\overrightarrow{u}, \overrightarrow{v}, \overrightarrow{w}[/imath] bất kì và mọi số thực [imath]k[/imath] ta có :
- [imath]\overrightarrow{u} \cdot \overrightarrow{v} = \overrightarrow{v} \cdot \overrightarrow{u}[/imath] (tính chất giao hoán)
- [imath]\overrightarrow{u}( \overrightarrow{v} + \overrightarrow{w}) = \overrightarrow{u} \cdot \overrightarrow{v} +\overrightarrow{u} \cdot \overrightarrow{w}[/imath] ( tính chất phân phối)
- [imath]( k \cdot \overrightarrow{ u} ) \cdot \overrightarrow{v} = ( k \cdot \overrightarrow{ u} \cdot \overrightarrow{v} ) = ( k \cdot \overrightarrow{ v} ) \cdot \overrightarrow{u}[/imath]