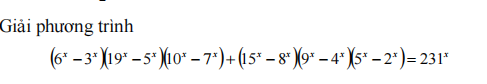zaa.
[imath](6^x-3^x)(19^x-5^x)(10^x-7^x)+(15^x-8^x)(9^x-4^x)(5^x-2^x)=231^x[/imath] (*)
TH1: [imath]x\le 0[/imath]
Khi đó [imath]6^x\le 3^x, 19^x\le 5^x, 10^x\le 7^x[/imath]
[imath]\Rightarrow (6^x-3^x)(19^x-5^x)(10^x-7^x)\le 0[/imath]
Tương tự ta có [imath](15^x-8^x)(9^x-4^x)(5^x-2^x)\le 0[/imath]
Suy ra [imath]VT\le 0[/imath] mà [imath]231^x>0[/imath] (vô nghiệm)
TH2: [imath]x>0[/imath]
Chia cả hai vế cho [imath]231^x=(3.7.11)^x[/imath]
(*)[imath]\iff (2^x-1)\left[(\dfrac{19}{11})^x-(\dfrac{5}{11})^x\right].\left[(\dfrac{10}{7})^x-1\right]+\left[(\dfrac{15}{11})^x-(\dfrac{8}{11})^x\right]\left[(\dfrac{9}{7})^x-(\dfrac{4}{7})^x\right]\left[(\dfrac{5}{3})^x-(\dfrac{2}{3})^x\right]=1[/imath]
Xét [imath]f(x)=(2^x-1)\left[(\dfrac{19}{11})^x-(\dfrac{5}{11})^x\right].\left[(\dfrac{10}{7})^x-1\right]+\left[(\dfrac{15}{11})^x-(\dfrac{8}{11})^x\right]\left[(\dfrac{9}{7})^x-(\dfrac{4}{7})^x\right]\left[(\dfrac{5}{3})^x-(\dfrac{2}{3})^x\right][/imath]
Ta sẽ cm được hàm số đồng biến
Mà [imath]f(1)=1\iff x=1[/imath] là nghiệm duy nhất của phương trình
Chị chưa nghĩ ra cách lớp 9, em xem tạm nhé
Ngoài ra, em xem thêm tại
[Lý thuyết] Chuyên đề HSG: Số học
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.