- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 25
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
- Khi giải bài toán hình không gian, đôi khi ta sẽ gặp 1 số bài mà rất khó để ta tìm ra được các tính chất hình học, các yếu tố đường vuông góc chung hay hình chiếu. vì thế để dễ dàng hơn trong việc giải toán, ta có thể gắn chúng vào trong hệ trục tọa độ Oxyz và vận dụng các kiến thức về phương pháp tọa độ để giải.
I. kiến thức cần có
- để giải hình không gian, chắc chắn bạn phải có kiến thức về hình không gian.
- kiến thức về phương pháp tọa độ trong không gian, bạn có thể tham khảo tại:
https://diendan.hocmai.vn/threads/toa-do-trong-khong-gian-va-kien-thuc-can-nho.744922/#post-3735191
II. cách xác định tọa độ điểm
1. điểm trên trục tọa độ
- Tìm tọa độ điểm A trên trục tọa độ ta tìm khoảng cách từ A đến gốc tọa độ và dựa
vào chiều dương đã chọn để xác định tọa độ A.
Ví dụ chọn tia O A trùng tia O x , điểm A và B nằm trên Ox
• OA = 2 ⇒ A (0;0;2).
• OB = 3 ⇒ B (0;0;-3) (do B nằm ở phần âm)

2. tọa độ điểm trên mặt phẳng tọa độ
-Tìm tọa độ của A trên 1 mặt phẳng tọa độ ta tìm hình chiếu của A trên các trục tọa
độ và dựa vào các tọa độ hình chiếu này để xác định tọa độ A.
Ví dụ: các điểm A,B,C có hình chiếu trên các trục với độ dài như hình vẽ, theo chiều dương
đã chọn ta được
• AK = 1 = [tex]x_K[/tex] , AH = 2 = [tex]y_K[/tex] : tọa độ A(1, 2)
• B I = 2 = −[tex]x_B[/tex] (do B nằm phần âm của trục hoành),BM = 1 = yB : tọa độ B(−2, 1)
• C J = 2,C M = 2: tọa độ C (−2,−2) (do C nằm ở phần âm của trục tung và trục hoành)

3. tọa đô trong trường hợp tổng quát
- Tìm tọa độ của A đầu tiên ta tìm tọa độ hình chiếu H của A lên mặt phẳng tọa độ
bất kì, sau đó ta tính độ dài AH . Tọa độ A xác định nhờ tọa độ H và độ dài AH .
Ví dụ tọa độ hình chiếu vuông góc của A lên mặt phẳng Oxy là H (a,b), ta tính được AH = c
thì khi đó A có tọa độ A(a,b, c ) (giả sử rằng các thành phần tọa độ A đều nằm trong phần
dương).
III. cách chọn hệ trục tọa độ
- Phần quan trọng nhất của phương pháp này là cách chọn hệ trục tọa độ. Không có
(phương pháp tổng quát, có nhiều hệ trục tọa độ có thể được chọn, chúng ta chọn
sao cho việc tìm tọa độ các điểm có nhiều số 0 càng tốt.
• Hệ trục tọa độ nằm trên 3 đường thẳng đôi 1 vuông góc nhau.
• Gốc tọa độ thường là chân đường cao của hình chóp, hình lăng trụ trùng với
đỉnh của hình vuông, hình chữ nhật, tam giác vuông hoặc có thể là trung điểm
của cạnh nào đó,...
IV. ví dụ minh họa cho phương pháp
1. cho chóp O.ABC có SA, SB, SC đôi một vuông góc và có độ dài lần lượt là a, b, c. điểm M cố định thuộc tam giác ABC có khoảng cách tới (OBC), (OAC),(OAB) lần lượt là 1, 2, 3. tìm a, b, c để thể tích khối chóp O.ABC đạt GTNN
Chọn hệ trục tọa độ như hình vẽ:
O(0;0;0), A(a;0;0), B(0;b;0), C(0;0;c) ( a, b, c > 0 )
từ dữ kiện khoảng cách ta suy ra tọa độ của M là M(1;2;3)
phương trình (ABC) theo đoạn chắn:
[tex]\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1[/tex]
M thuộc (ABC) nên: [tex]\frac{1}{a}+\frac{2}{b}+\frac{3}{c}=1[/tex]
theo bất đẳng thức cauchuy:
[tex]\frac{1}{a}+\frac{2}{b}+\frac{3}{c}\geq 3\sqrt[3]{\frac{6}{abc}}<=>1\geq 3\sqrt[3]{\frac{6}{abc}}<=>abc\geq 162<=>V=\frac{1}{6}abc\geq 27[/tex]
dấu bằng xảy ra khi [tex]\frac{1}{a}=\frac{2}{b}=\frac{3}{c}=\frac{1}{3}[/tex]

2. Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. AA'=2a và vuông góc với (ABC). D là trung điểm BB', M di động trên AA'. tìm giá trị lớn nhất và nhỏ nhất của diện tích tam giác C'DM.
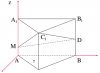
chọn hệ trục tọa độ sao cho A trùng O, [tex]B\in Oy, A'\in Oz[/tex]
khi đó A(0;0;0), A'(0;0;2a), B(0;a;0), B'(0;a;2a), [tex]C'(\frac{a\sqrt{3}}{2};\frac{a}{2};2a)[/tex], D(0;a;a).
do M di động trên AA' nên M(0;0;t) với [tex]t\in [0;2a][/tex]
ta có:
[tex]S_{C'DM}=\frac{1}{2}|[\overrightarrow{DC'}.\overrightarrow{DM}]|[/tex]
với [tex]\left\{\begin{matrix} \overrightarrow{DC'}(\frac{a\sqrt{3}}{2};-\frac{a}{2};a)\\ \overrightarrow{DM}(0;-a;t-a) \end{matrix}\right. =>S=\frac{1}{2}.\frac{a}{2}.\sqrt{4t^2-12at+15a^2}[/tex]
xét [tex]f(t)=4t^2-12at+15a^2[/tex]
suy ra [tex]S_{max}=\frac{a^2\sqrt{15}}{4}<=>t=0[/tex] hay M trùng A
I. kiến thức cần có
- để giải hình không gian, chắc chắn bạn phải có kiến thức về hình không gian.
- kiến thức về phương pháp tọa độ trong không gian, bạn có thể tham khảo tại:
https://diendan.hocmai.vn/threads/toa-do-trong-khong-gian-va-kien-thuc-can-nho.744922/#post-3735191
II. cách xác định tọa độ điểm
1. điểm trên trục tọa độ
- Tìm tọa độ điểm A trên trục tọa độ ta tìm khoảng cách từ A đến gốc tọa độ và dựa
vào chiều dương đã chọn để xác định tọa độ A.
Ví dụ chọn tia O A trùng tia O x , điểm A và B nằm trên Ox
• OA = 2 ⇒ A (0;0;2).
• OB = 3 ⇒ B (0;0;-3) (do B nằm ở phần âm)
2. tọa độ điểm trên mặt phẳng tọa độ
-Tìm tọa độ của A trên 1 mặt phẳng tọa độ ta tìm hình chiếu của A trên các trục tọa
độ và dựa vào các tọa độ hình chiếu này để xác định tọa độ A.
Ví dụ: các điểm A,B,C có hình chiếu trên các trục với độ dài như hình vẽ, theo chiều dương
đã chọn ta được
• AK = 1 = [tex]x_K[/tex] , AH = 2 = [tex]y_K[/tex] : tọa độ A(1, 2)
• B I = 2 = −[tex]x_B[/tex] (do B nằm phần âm của trục hoành),BM = 1 = yB : tọa độ B(−2, 1)
• C J = 2,C M = 2: tọa độ C (−2,−2) (do C nằm ở phần âm của trục tung và trục hoành)

3. tọa đô trong trường hợp tổng quát
- Tìm tọa độ của A đầu tiên ta tìm tọa độ hình chiếu H của A lên mặt phẳng tọa độ
bất kì, sau đó ta tính độ dài AH . Tọa độ A xác định nhờ tọa độ H và độ dài AH .
Ví dụ tọa độ hình chiếu vuông góc của A lên mặt phẳng Oxy là H (a,b), ta tính được AH = c
thì khi đó A có tọa độ A(a,b, c ) (giả sử rằng các thành phần tọa độ A đều nằm trong phần
dương).
III. cách chọn hệ trục tọa độ
- Phần quan trọng nhất của phương pháp này là cách chọn hệ trục tọa độ. Không có
(phương pháp tổng quát, có nhiều hệ trục tọa độ có thể được chọn, chúng ta chọn
sao cho việc tìm tọa độ các điểm có nhiều số 0 càng tốt.
• Hệ trục tọa độ nằm trên 3 đường thẳng đôi 1 vuông góc nhau.
• Gốc tọa độ thường là chân đường cao của hình chóp, hình lăng trụ trùng với
đỉnh của hình vuông, hình chữ nhật, tam giác vuông hoặc có thể là trung điểm
của cạnh nào đó,...
IV. ví dụ minh họa cho phương pháp
1. cho chóp O.ABC có SA, SB, SC đôi một vuông góc và có độ dài lần lượt là a, b, c. điểm M cố định thuộc tam giác ABC có khoảng cách tới (OBC), (OAC),(OAB) lần lượt là 1, 2, 3. tìm a, b, c để thể tích khối chóp O.ABC đạt GTNN
Chọn hệ trục tọa độ như hình vẽ:
O(0;0;0), A(a;0;0), B(0;b;0), C(0;0;c) ( a, b, c > 0 )
từ dữ kiện khoảng cách ta suy ra tọa độ của M là M(1;2;3)
phương trình (ABC) theo đoạn chắn:
[tex]\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1[/tex]
M thuộc (ABC) nên: [tex]\frac{1}{a}+\frac{2}{b}+\frac{3}{c}=1[/tex]
theo bất đẳng thức cauchuy:
[tex]\frac{1}{a}+\frac{2}{b}+\frac{3}{c}\geq 3\sqrt[3]{\frac{6}{abc}}<=>1\geq 3\sqrt[3]{\frac{6}{abc}}<=>abc\geq 162<=>V=\frac{1}{6}abc\geq 27[/tex]
dấu bằng xảy ra khi [tex]\frac{1}{a}=\frac{2}{b}=\frac{3}{c}=\frac{1}{3}[/tex]

2. Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. AA'=2a và vuông góc với (ABC). D là trung điểm BB', M di động trên AA'. tìm giá trị lớn nhất và nhỏ nhất của diện tích tam giác C'DM.

chọn hệ trục tọa độ sao cho A trùng O, [tex]B\in Oy, A'\in Oz[/tex]
khi đó A(0;0;0), A'(0;0;2a), B(0;a;0), B'(0;a;2a), [tex]C'(\frac{a\sqrt{3}}{2};\frac{a}{2};2a)[/tex], D(0;a;a).
do M di động trên AA' nên M(0;0;t) với [tex]t\in [0;2a][/tex]
ta có:
[tex]S_{C'DM}=\frac{1}{2}|[\overrightarrow{DC'}.\overrightarrow{DM}]|[/tex]
với [tex]\left\{\begin{matrix} \overrightarrow{DC'}(\frac{a\sqrt{3}}{2};-\frac{a}{2};a)\\ \overrightarrow{DM}(0;-a;t-a) \end{matrix}\right. =>S=\frac{1}{2}.\frac{a}{2}.\sqrt{4t^2-12at+15a^2}[/tex]
xét [tex]f(t)=4t^2-12at+15a^2[/tex]
suy ra [tex]S_{max}=\frac{a^2\sqrt{15}}{4}<=>t=0[/tex] hay M trùng A


