- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 25
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. định nghĩa
- cho điểm I cố định và số thực k không đổi. khi đó, nếu điểm M' thỏa mãn:
[tex]\overrightarrow{IM}=k.\overrightarrow{IM'}[/tex]
thì gọi là phép vị tự tâm I, tỉ số k.
- M' là ảnh của M qua phép vị tự tâm I, tỉ số k.
[tex]V_{(I,k)}(M)=M'<=>\overrightarrow{IM}=k.\overrightarrow{IM'}[/tex]
- phép vị tự với tỉ số vị tự k=-1 [tex]V_{(I,1)}[/tex] là phép đồng nhất.
- phép vị tự với tỉ số vị tự k=-1 [tex]V_{(I,-1)}[/tex] là phép đối xứng tâm I.
- nếu [tex]k\neq 1[/tex] và [tex]V_{(I,k)}(M)=M<=>I\equiv M[/tex]
2. tính chất của phép vị tự
- phép vị tự biến 1 vecto thành 1 vecto có độ lớn bằng |k| vecto ban đầu.
- phép vị tự biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi vị trí trí giữa chúng.
- biến đa giác thành đa giác đồng dạng với đa giác đã cho theo tỉ số |k|.
- biến đường tròn thành đường tròn có bán kính R'=|k|.R. khi đó, ta chỉ cần xác định ảnh của tâm qua phép vị tự.
3. biểu thức tọa độ
- cho phép vị tự tâm I(a;b) theo tỉ số k. khi đó, ảnh của M(x;y) qua phép vị tự tâm I tỉ số k là M'(x';y').
[tex]\left\{\begin{matrix} x'=kx+(1-k).a\\ y'=ky+(1-k).b \end{matrix}\right.[/tex]
4. tâm vị tự của 2 đường tròn
- cho 2 đường tròn C(O,R) và C'(O',R').
gọi OM và OM' lần lượt là 2 bán kính của (C) và (C') sao cho 2 vecto [tex]\overrightarrow{OM},\overrightarrow{OM'}[/tex] cùng chiều.
+ nếu [tex]OO'\cap MM'=I[/tex] thì I là tâm vị tự của phép vị tự [tex]V_{(I,\frac{R'}{R})}[/tex]
-> I là tâm vị tự trong.
nếu [tex]OO'\cap M_1M'=I\left ( M_1=D_O(M) \right )[/tex] thì I là tâm vị tự của phép vị tự [tex]V_{(I,-\frac{R'}{R})}[/tex]
-> I là tâm vị tự ngoài.
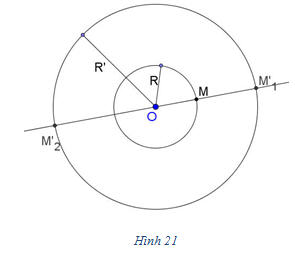
+ nếu O trùng O', thì cả 2 phép vị tự [tex]V_{(O,\frac{R'}{R})}[/tex] và [tex]V_{(O,-\frac{R'}{R})}[/tex] biến đường tròn (C) thành đường tròn (C').
- cho điểm I cố định và số thực k không đổi. khi đó, nếu điểm M' thỏa mãn:
[tex]\overrightarrow{IM}=k.\overrightarrow{IM'}[/tex]
thì gọi là phép vị tự tâm I, tỉ số k.
- M' là ảnh của M qua phép vị tự tâm I, tỉ số k.
[tex]V_{(I,k)}(M)=M'<=>\overrightarrow{IM}=k.\overrightarrow{IM'}[/tex]
- phép vị tự với tỉ số vị tự k=-1 [tex]V_{(I,1)}[/tex] là phép đồng nhất.
- phép vị tự với tỉ số vị tự k=-1 [tex]V_{(I,-1)}[/tex] là phép đối xứng tâm I.
- nếu [tex]k\neq 1[/tex] và [tex]V_{(I,k)}(M)=M<=>I\equiv M[/tex]
2. tính chất của phép vị tự
- phép vị tự biến 1 vecto thành 1 vecto có độ lớn bằng |k| vecto ban đầu.
- phép vị tự biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi vị trí trí giữa chúng.
- biến đa giác thành đa giác đồng dạng với đa giác đã cho theo tỉ số |k|.
- biến đường tròn thành đường tròn có bán kính R'=|k|.R. khi đó, ta chỉ cần xác định ảnh của tâm qua phép vị tự.
3. biểu thức tọa độ
- cho phép vị tự tâm I(a;b) theo tỉ số k. khi đó, ảnh của M(x;y) qua phép vị tự tâm I tỉ số k là M'(x';y').
[tex]\left\{\begin{matrix} x'=kx+(1-k).a\\ y'=ky+(1-k).b \end{matrix}\right.[/tex]
4. tâm vị tự của 2 đường tròn
- cho 2 đường tròn C(O,R) và C'(O',R').
gọi OM và OM' lần lượt là 2 bán kính của (C) và (C') sao cho 2 vecto [tex]\overrightarrow{OM},\overrightarrow{OM'}[/tex] cùng chiều.
+ nếu [tex]OO'\cap MM'=I[/tex] thì I là tâm vị tự của phép vị tự [tex]V_{(I,\frac{R'}{R})}[/tex]
-> I là tâm vị tự trong.
nếu [tex]OO'\cap M_1M'=I\left ( M_1=D_O(M) \right )[/tex] thì I là tâm vị tự của phép vị tự [tex]V_{(I,-\frac{R'}{R})}[/tex]
-> I là tâm vị tự ngoài.
+ nếu O trùng O', thì cả 2 phép vị tự [tex]V_{(O,\frac{R'}{R})}[/tex] và [tex]V_{(O,-\frac{R'}{R})}[/tex] biến đường tròn (C) thành đường tròn (C').
