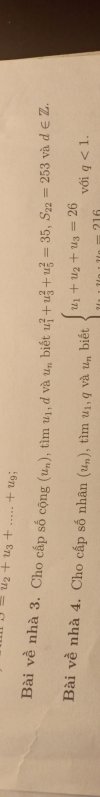- 7 Tháng tám 2018
- 2,945
- 7,443
- 621
- 19
- Lào Cai
- Trường THPT số 1 Lào Cai
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
gip em trong ngày hôm nay ạ, trước 22h là đc ạ
Bài 3: Cho cấp số cộng [imath](u_n)[/imath]. Tìm [imath]u_1; d[/imath] và [imath]u_n[/imath] biết [imath]u_1^2 + u_3^2 + u_5^2 = 35; S_{22} = 253[/imath] và [imath]d \in \Z[/imath]
Bài 4:
Bài 5: Cho 3 số tạo thành 1 cấp số cộng có tổng bằng 21. Nếu thêm [imath]2;3;9[/imath] lần lượt vào số thứ nhất, số thứ 2, số thứ 3 thì tạo thành 1 cấp số nhân. Tìm 3 số đó
Bài 6: Ba số khác nhau có tổng bằng 171 có thể coi là 3 số hạng liên tiếp của 1 cấp số nhân, hoặc coi là các số hạng thứ 3, thứ 5 và thứ 19 của một cấp số cộng. Tìm các số đó?
Bài 3: Cho cấp số cộng [imath](u_n)[/imath]. Tìm [imath]u_1; d[/imath] và [imath]u_n[/imath] biết [imath]u_1^2 + u_3^2 + u_5^2 = 35; S_{22} = 253[/imath] và [imath]d \in \Z[/imath]
Bài 4:
Bài 5: Cho 3 số tạo thành 1 cấp số cộng có tổng bằng 21. Nếu thêm [imath]2;3;9[/imath] lần lượt vào số thứ nhất, số thứ 2, số thứ 3 thì tạo thành 1 cấp số nhân. Tìm 3 số đó
Bài 6: Ba số khác nhau có tổng bằng 171 có thể coi là 3 số hạng liên tiếp của 1 cấp số nhân, hoặc coi là các số hạng thứ 3, thứ 5 và thứ 19 của một cấp số cộng. Tìm các số đó?
Attachments
Last edited by a moderator: