- 13 Tháng bảy 2017
- 3,419
- 3
- 4,467
- 644
- 21
- Bình Định
- THPT Chuyên Lê Quý Đôn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào cả nhà nhé ^^ Một mùa Noel nữa lại sắp đến rồi... không biết Santa Claus đã tặng quà cho các em chưa nhỉ 
Đừng lo, chị ở đây để tặng trước cho các em nè!!!
Đối với học sinh đang có nhu cầu/đang ôn thi chuyên Lí, thật là mệt mỏi và bơ phờ vì học Lí mà toàn thấy Toán. Vì thương các em toii khóc ròng, hôm nay chiếc topic này ra đời
I/ Mục đích
- Giúp các bạn có niềm đam mê với Vật Lý không còn sợ Toán
- Hỗ trợ cho kì thi tuyển sinh vào 10 sắp tới
- Nhằm giúp các bạn biết thêm những cách làm hay trong các bài toán Vật Lý
II/ Nội dung
- Chi tiết lý thuyết các phần toán quan trọng
- Các công thức và cách dùng liên quan
- Bài tập và hướng dẫn giải chi tiết theo hướng áp dụng phương pháp toán
Okay không dong dài nữa, thời gian bây giờ là vàng bạc với các em toii, mình vô liền thuii ~~
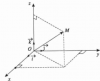
Trong Vật Lý có rất nhiều đại lượng cần đến vecto.
Vector là một đại lượng biểu diễn cho cả độ lớn và hướng.
Ví dụ như để biểu diễn một lực nào đó tác dụng lên vật, ta có một vector gồm có 2 thành phần – độ lớn lực tác động lên vật đó và hướng tác động. Hay ta có thể dùng vector để biểu diễn vận tốc – tốc độ và hướng. Ngoài ra, ta còn có dạng vector thuần chỉ hướng. Đơn cử như việc diễn tả hướng nhìn của một camera trong không gian, hay ta muốn ám chỉ đến hướng mà ánh sáng di chuyển trong không gian.
Trong phần này, mình sẽ đề câp chủ yếu về cộng vận tốc, còn về phần phân tích và hợp lực [imath]\vec{F}[/imath] tác dụng thì lên đầu lớp 10 các em sẽ được học kĩ hơn sau nha.
II/ Tính tương đối của chuyển động
1. Tính tương đối của quỹ đạo
Hình dạng quỹ đạo của chuyển động trong các hệ quy chiếu khác nhau thì khác nhau - quỹ đạo có tính tương đối
2. Tính tương đối của vận tốc
Vận tốc của vật chuyển động đối với các hệ quy chiếu khác nhau thì khác nhau - vận tốc có tính tương đối
Vậy hệ qui chiếu là gì?
Hệ quy chiếu: gồm HQC đứng yên và HQC chuyển động
Hệ qui chiếu là cột mốc quan trọng trong vật lí cơ bản, dùng để xác định trạng thái, vị trí của một đối tượng nghiên cứu trong vật lí học. Bao gồm hai khái niệm sau:
- Gốc thời gian (mốc thời gian): là một mốc dùng để xác định khi nào tính thời gian
III/ Công thức cộng vận tốc
1. Trường hợp các vận tốc cùng phương cùng chiều
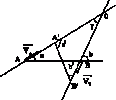
[imath]\vec{v_{tb}} = \vec{v_{tn}} + \vec{v_{nb}}[/imath]
Trong đó:
[imath]\vec{v_{tb}}[/imath] : vận tốc của thuyền đối với bờ
[imath]\vec{v_{tn}}[/imath] : vận tốc của thuyền đối với nước
[imath]\vec{v_{nb}}[/imath] : vận tốc của nước đối với bờ
Công thức cộng vận tốc: [imath]\vec{v_{13}} = \vec{v_{12}} + \vec{v_{23}}[/imath]
Về độ lớn: [imath]|v_{13}| = |v_{12}| + |v_{23}|[/imath]
Với số 1 ứng với vật chuyển động, số 2 ứng với hệ quy chiếu chuyển động, số 3 ứng với hệ quy chiếu đứng yên.
2. Trường hợp các vận tốc cùng phương ngược chiều
Tương tự ta sẽ có công thức cộng vận tốc ở đây là:
[imath]\vec{v_{13}} = \vec{v_{12}} + \vec{v_{23}}[/imath]
Nhưng độ lớn sẽ là: [imath]|v_{13}| = |v_{12}| - |v_{23}|[/imath]
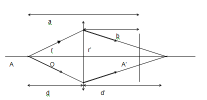
3. Tổng quát
Công thức cộng vận tốc tổng quát:
● Số 1 gắn với vật cần tính vận tốc.
● Số hai gắn với hệ quy chiếu là các vật chuyển động.
● Số 3 gắn với hệ quy chiếu là các vật đứng yên.
● [imath]v_{12}[/imath] là vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối
● [imath]v_{23}[/imath] là vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo.
● [imath]v_{13}[/imath] là vận tốc của vật so với hệ quy chiếu đứng yên gọi là vận tốc tuyệt đối.
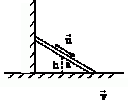
● Độ lớn của vận tốc: [imath]v_{13}= \sqrt{v_{12}^{2}+v_{23}^{2}+2.v_{12}^{2}.v_{23}^{2}.cos\alpha }[/imath]
- Trong đó: a là góc hợp bởi [imath]v_{12}[/imath] và [imath]v_{23}[/imath]
● Trường hợp đặc biệt:
[imath]v_{12}[/imath] cùng chiều [imath]v_{23}[/imath] thì: [imath]v_{13} = v_{12} + v_{23}[/imath]
[imath]v_{12}[/imath] ngược chiều [imath]v_{23}[/imath] thì: [imath]v_{13}= |v_{12} - v_{23}|[/imath]
[imath]v_{12}[/imath] vuông góc [imath]v_{23}[/imath] thì:
[imath]v_{13}[/imath] = [imath]\sqrt{v_{12}^{2}+v_{23}^{2}}[/imath]
Trong đó [imath]\alpha[/imath] là góc hợp bởi [imath]\vec{v_{12}}[/imath] và [imath]\vec{v_{23}}[/imath]
Một số bài toàn ứng dụng phần kiến thức "Cộng vận tốc"
Bài 1:
Một chiếc thuyền xuôi dòng từ A đến B, vận tốc của dòng nước là 5km/h. Tính vận tốc của thuyền so với dòng nước và chiều dài từ A đến B biết thuyền xuôi dòng mất 2 giờ và ngược dòng mất 3 giờ trên cùng đoạn đường AB.
Bài 2:
Trên một tuyến đường xe buýt thẳng, các xe buýt chuyển động theo 1 chiều và cách đều nhau 5km. Một người đi xe đạp chuyển động thẳng đều trên tuyến đường này. Nếu đi theo một chiều thì tại thời điểm t=0, người đi xe đạp gặp xe buýt thứ nhất, đến thời điểm t=1h , người này gặp xe buýt thứ 12. Nếu đi theo chiều ngược lại thì thời điểm t=0, người đi xe đạp gặp xe buýt thứ nhất, đến thời điểm t=1h người này gặp xe buýt thứ 6. Hỏi nếu người này đứng yên bên đường thì trong 1 giờ tính từ thời điểm gặp xe buýt thứ nhất, người này còn gặp được bao nhiều xe buýt nữa ? Bỏ qua kích thước của xe buýt và xe đạp.
Bài 3:
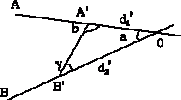
Một ca nô chạy qua sông xuất phát từ A, mũi hướng đến B ở bờ bên kia (AB vuông góc với bờ sông) nhưng do nước chảy nên khi đến bên kia ca nô ở lại C cách B một đoạn BC=200 m. thời gian qua sông là 100s. Ở lần qua sống thứ hai nếu người lái giữ cho mũi ca nô chếch 60 độ so với bờ sông và mở máy chạy như trước thì ca nô đến đúng B.
a/ Tính vận tốc dòng nước và vận tốc của ca nô.
b/ Tính bề rộng của dòng sông
c/ Tính thời gian qua sông của ca nô ở lần thứ hai.
Các em cứ thỏa sức làm nhé, đáp án chị sẽ cập nhật sau @manh huy @nguyenbinhducdat @Chris Master Harry @Beo'S @Cao Hải Nam
Đừng lo, chị ở đây để tặng trước cho các em nè!!!Đối với học sinh đang có nhu cầu/đang ôn thi chuyên Lí, thật là mệt mỏi và bơ phờ vì học Lí mà toàn thấy Toán. Vì thương các em toii khóc ròng, hôm nay chiếc topic này ra đời
NHỮNG KIẾN THỨC TOÁN QUAN TRỌNG (PHẦN 1) 
I/ Mục đích
- Giúp các bạn có niềm đam mê với Vật Lý không còn sợ Toán
- Hỗ trợ cho kì thi tuyển sinh vào 10 sắp tới
- Nhằm giúp các bạn biết thêm những cách làm hay trong các bài toán Vật Lý
II/ Nội dung
- Chi tiết lý thuyết các phần toán quan trọng
- Các công thức và cách dùng liên quan
- Bài tập và hướng dẫn giải chi tiết theo hướng áp dụng phương pháp toán
Okay không dong dài nữa, thời gian bây giờ là vàng bạc với các em toii, mình vô liền thuii ~~
PHƯƠNG PHÁP CỘNG VECTO
I/ Lý do?
Trong Vật Lý có rất nhiều đại lượng cần đến vecto.
Vector là một đại lượng biểu diễn cho cả độ lớn và hướng.
Ví dụ như để biểu diễn một lực nào đó tác dụng lên vật, ta có một vector gồm có 2 thành phần – độ lớn lực tác động lên vật đó và hướng tác động. Hay ta có thể dùng vector để biểu diễn vận tốc – tốc độ và hướng. Ngoài ra, ta còn có dạng vector thuần chỉ hướng. Đơn cử như việc diễn tả hướng nhìn của một camera trong không gian, hay ta muốn ám chỉ đến hướng mà ánh sáng di chuyển trong không gian.
Trong phần này, mình sẽ đề câp chủ yếu về cộng vận tốc, còn về phần phân tích và hợp lực [imath]\vec{F}[/imath] tác dụng thì lên đầu lớp 10 các em sẽ được học kĩ hơn sau nha.
II/ Tính tương đối của chuyển động
1. Tính tương đối của quỹ đạo
Hình dạng quỹ đạo của chuyển động trong các hệ quy chiếu khác nhau thì khác nhau - quỹ đạo có tính tương đối
2. Tính tương đối của vận tốc
Vận tốc của vật chuyển động đối với các hệ quy chiếu khác nhau thì khác nhau - vận tốc có tính tương đối
Vậy hệ qui chiếu là gì?
Hệ quy chiếu: gồm HQC đứng yên và HQC chuyển động
Hệ qui chiếu là cột mốc quan trọng trong vật lí cơ bản, dùng để xác định trạng thái, vị trí của một đối tượng nghiên cứu trong vật lí học. Bao gồm hai khái niệm sau:
- Hệ trục tọa độ - gốc tọa độ: đối với không gian 2 hoặc 3 chiều
- Đồng hồ đo và mốc thời gian
- Gốc thời gian (mốc thời gian): là một mốc dùng để xác định khi nào tính thời gian
III/ Công thức cộng vận tốc
1. Trường hợp các vận tốc cùng phương cùng chiều
Trong đó:
[imath]\vec{v_{tb}}[/imath] : vận tốc của thuyền đối với bờ
[imath]\vec{v_{tn}}[/imath] : vận tốc của thuyền đối với nước
[imath]\vec{v_{nb}}[/imath] : vận tốc của nước đối với bờ
Công thức cộng vận tốc: [imath]\vec{v_{13}} = \vec{v_{12}} + \vec{v_{23}}[/imath]
Về độ lớn: [imath]|v_{13}| = |v_{12}| + |v_{23}|[/imath]
Với số 1 ứng với vật chuyển động, số 2 ứng với hệ quy chiếu chuyển động, số 3 ứng với hệ quy chiếu đứng yên.
2. Trường hợp các vận tốc cùng phương ngược chiều
[imath]\vec{v_{13}} = \vec{v_{12}} + \vec{v_{23}}[/imath]
Nhưng độ lớn sẽ là: [imath]|v_{13}| = |v_{12}| - |v_{23}|[/imath]
3. Tổng quát
Công thức cộng vận tốc tổng quát:
[tex]\vec{v_{13}} = \vec{v_{12}} + \vec{v_{23}}[/tex]
- Trong đó:● Số 1 gắn với vật cần tính vận tốc.
● Số hai gắn với hệ quy chiếu là các vật chuyển động.
● Số 3 gắn với hệ quy chiếu là các vật đứng yên.
● [imath]v_{12}[/imath] là vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối
● [imath]v_{23}[/imath] là vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo.
● [imath]v_{13}[/imath] là vận tốc của vật so với hệ quy chiếu đứng yên gọi là vận tốc tuyệt đối.
● Độ lớn của vận tốc: [imath]v_{13}= \sqrt{v_{12}^{2}+v_{23}^{2}+2.v_{12}^{2}.v_{23}^{2}.cos\alpha }[/imath]
- Trong đó: a là góc hợp bởi [imath]v_{12}[/imath] và [imath]v_{23}[/imath]
● Trường hợp đặc biệt:
[imath]v_{12}[/imath] cùng chiều [imath]v_{23}[/imath] thì: [imath]v_{13} = v_{12} + v_{23}[/imath]
[imath]v_{12}[/imath] ngược chiều [imath]v_{23}[/imath] thì: [imath]v_{13}= |v_{12} - v_{23}|[/imath]
[imath]v_{12}[/imath] vuông góc [imath]v_{23}[/imath] thì:
[imath]v_{13}[/imath] = [imath]\sqrt{v_{12}^{2}+v_{23}^{2}}[/imath]
Trong đó [imath]\alpha[/imath] là góc hợp bởi [imath]\vec{v_{12}}[/imath] và [imath]\vec{v_{23}}[/imath]
Một số bài toàn ứng dụng phần kiến thức "Cộng vận tốc"
Bài 1:
Một chiếc thuyền xuôi dòng từ A đến B, vận tốc của dòng nước là 5km/h. Tính vận tốc của thuyền so với dòng nước và chiều dài từ A đến B biết thuyền xuôi dòng mất 2 giờ và ngược dòng mất 3 giờ trên cùng đoạn đường AB.
Bài 2:
Trên một tuyến đường xe buýt thẳng, các xe buýt chuyển động theo 1 chiều và cách đều nhau 5km. Một người đi xe đạp chuyển động thẳng đều trên tuyến đường này. Nếu đi theo một chiều thì tại thời điểm t=0, người đi xe đạp gặp xe buýt thứ nhất, đến thời điểm t=1h , người này gặp xe buýt thứ 12. Nếu đi theo chiều ngược lại thì thời điểm t=0, người đi xe đạp gặp xe buýt thứ nhất, đến thời điểm t=1h người này gặp xe buýt thứ 6. Hỏi nếu người này đứng yên bên đường thì trong 1 giờ tính từ thời điểm gặp xe buýt thứ nhất, người này còn gặp được bao nhiều xe buýt nữa ? Bỏ qua kích thước của xe buýt và xe đạp.
Bài 3:
Một ca nô chạy qua sông xuất phát từ A, mũi hướng đến B ở bờ bên kia (AB vuông góc với bờ sông) nhưng do nước chảy nên khi đến bên kia ca nô ở lại C cách B một đoạn BC=200 m. thời gian qua sông là 100s. Ở lần qua sống thứ hai nếu người lái giữ cho mũi ca nô chếch 60 độ so với bờ sông và mở máy chạy như trước thì ca nô đến đúng B.
a/ Tính vận tốc dòng nước và vận tốc của ca nô.
b/ Tính bề rộng của dòng sông
c/ Tính thời gian qua sông của ca nô ở lần thứ hai.
Các em cứ thỏa sức làm nhé, đáp án chị sẽ cập nhật sau @manh huy @nguyenbinhducdat @Chris Master Harry @Beo'S @Cao Hải Nam
