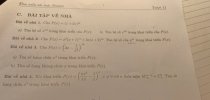Bài 4:
[imath]5C^{n-1}_n=C^3_n[/imath]
[imath]\Leftrightarrow 5C^1_n=\dfrac{n(n-1)(n-2)}{3!}[/imath]
[imath]\Leftrightarrow 30n=n(n^2-3n+2)[/imath]
[imath]\Leftrightarrow n^3-3n^2-28n=0[/imath]
[imath]\Leftrightarrow n=7[/imath]
[imath]P(x)=\left(\dfrac{x^2}2-\dfrac{1}x\right)^7[/imath]
[imath]=\displaystyle \sum^{11}_{k=0}C^{k}_7 \dfrac{x^{2k}}{2^k}\dfrac{(-1)^{7-k}}{x^{7-k}}=\displaystyle \sum^{11}_{k=0} C^k_7 \dfrac{(-1)^{7-k}}{2^k}x^{3k-7}[/imath]
[imath]x^5[/imath] thì [imath]3k-7=5\Leftrightarrow k=4[/imath]
Vậy hệ số của [imath]x^5[/imath] là [imath]\dfrac{-C^4_7}{16}[/imath]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.