[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Là một phương pháp hay nhưng ít học sinh sử dụng bổ trợ cho bài tập mạch điện khó dành cho học sinh giỏi không chuyên. Phương pháp mạch tương đương 
Mạch, nguồn tương đương nghe tưởng chừng rất quen thuộc, nhưng trong chủ đề lần này sẽ được đưa lên 1 tầm cao mới!! .
Bằng cách ghép các phần phụ kiện không thực sự liên quan đến bài toàn, làm tối giản mạch điện, để áp dụng tính toán một cách nhanh nhất. Chúng ta có thể hiểu qua một ví dụ sau:
Bằng cách ghép điện trở [imath]R_0[/imath] vào nguồn điện ta được một mạch điện mới với nguồn điện mới có : [imath]\left\{\begin{matrix} E=E\\ r'=r+R_0 \end{matrix}\right.[/imath]
Đây chỉ là một ví dụ đơn giản để ta thấy dễ hiểu và tiếp cận dễ hơn về phương pháp này, thực ra nó cũng dễ mà
Ta sẽ tổng hợp những trường hợp cơ bản nhất mà cũng dùng nhiều nhất nhé !!
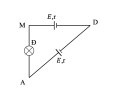
Cho bài toán: Cho mạch điện như hình vẽ, các nguồn có suất điện động và điện trở trong tương ứng là [imath]\left(e_{1} ; r_{1}\right) ;\left(e_{2} ; r_{2}\right) ; \ldots .\left(e_{n} ; r_{n}\right)[/imath]. Để đơn giản, ta giả sử các nguồn có cực dương nối với [imath]A[/imath] trừ nguồn [imath]\left(e_{2} ; r_{2}\right)[/imath]. Tìm suất điện động và điện trở trong của bộ nguồn này nếu coi [imath]A[/imath] và [imath]B[/imath] là hai cực của nguồn điện tương đương.
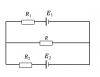
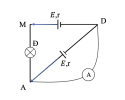
1.Nguồn địện tương đương của bộ nguồn mắc nối tiếp (H.1)
[imath]\left\{\begin{matrix} e_b=e_1-e_2+e_3+...+e_n \\ r_b=r_1+r_2+r_3+...+r_n \end{matrix}\right.[/imath]
*Đặc biệt nếu chỉ gồm điện trở [imath]R[/imath] mắc nối tiếp bộ bộ ta xem nó như một nguồn điện có [imath]e_R=0,r=R[/imath]
[imath]\Rightarrow \left\{\begin{matrix} e_b=e \\r_b=r+R \end{matrix}\right.[/imath]
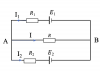
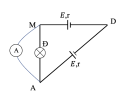
2.Nguồn điện tương đương của bộ nguồn ghép song song (H.2)
Công thức bộ nguồn như sau:[imath]\left\{\begin{matrix} \dfrac{1}{r_b}=\dfrac{1}{r_1}+\dfrac{1}{r_2}+...+\dfrac{1}{r_n}\\ \dfrac{e}{r_b}=\dfrac{e_1}{r_1}+\dfrac{e_2}{r_2}+...+\dfrac{e_n}{r_n} \end{matrix}\right.[/imath]
Chứng minh:
Giả sử cả bộ nguồn ở hình H.2 tương đương với nguồn bộ nguồn [imath](e_b;r_b)[/imath]
Ta có định lí nút tại [imath]A[/imath] :
[imath]I=I_1-I_2+I_3+...+I_n[/imath]
[imath]\Rightarrow \dfrac{e_b-U}{r_b}=\dfrac{e_1-U}{r_1}-\dfrac{e_2+U}{r_2}+...+\dfrac{e_n-U}{r_n}[/imath]
[imath]\Rightarrow \dfrac{e_b-U}{r_b}=(\dfrac{e_1}{r_1}-\dfrac{e_2}{r_2}+...+\dfrac{e_n}{r_n})-(\dfrac{U}{r_1}+\dfrac{U}{r_2}+...+\dfrac{U}{r_n})[/imath]
Đồng nhất hệ số ta được điều cần chứng minh trên!!
*Đặc biệt nếu được mắc song song với một điện trở thuần [imath]R[/imath] khác, ta có thể quy chuẩn nó là một nguồn địên với [imath]e_R=0,r=R[/imath]
Áp dụng ngay vào một số bài toán để thấy sự hiểu quả nhé:
Cách giải thông thường:
Ta có: [imath]I=\dfrac{ER}{r+R_{2}+\dfrac{R_{1} R_{2}}{R_{1}+R_{2}}}=\dfrac{12}{5+\dfrac{5 x}{5+x}}=\dfrac{12(5+x)}{(25+10 x)}[/imath]
Áp dụng công thức chia dòng ta được dòng qua [imath]R_{2}: I_{2}=\dfrac{R_{1}}{R_{1}+R_{2}} I=\dfrac{5}{5+x} \dfrac{12(5+x)}{(25+10 x)}=\dfrac{12}{5+2 x}[/imath]
Công suất trên [imath]R_{2}[/imath] là :
[imath]P_{2}=R_{2} I_{2}^{2}=x\left(\dfrac{12}{5+2 x}\right)^{2}=\dfrac{144 x}{(5+2 x)^{2}}=\dfrac{144 x}{(2 x-5)^{2}+40 x}=\dfrac{144}{\left(\dfrac{(2 x-5)^{2}}{x}+40\right)}[/imath]
Vậy [imath]P_{2 \max }[/imath] khi [imath]2 x=5=>x=2,5 \Omega[/imath]
Áp dụng phương pháp nguồn tương đương:
Mục tiêu biến mạch điện thành một mạch mới mà điện trở ngoài chỉ gồm [imath]R_2[/imath] và áp dụng hệ quả cực trị phụ quen thuộc:
Nếu là trắc nghiệm thì phương pháp 2 ưu việt hơn hẳn còn khi thi tự luận ở mọi bước từ công thức nguồn tương đương đến hệ quả cực trị các bạn đều phải chứng minh hết mới được áp dung nhé, đây chưa phải là những gì hay nhất về phương pháp này , hẹn các bạn ở số sau
Mạch, nguồn tương đương nghe tưởng chừng rất quen thuộc, nhưng trong chủ đề lần này sẽ được đưa lên 1 tầm cao mới!! .
Bằng cách ghép các phần phụ kiện không thực sự liên quan đến bài toàn, làm tối giản mạch điện, để áp dụng tính toán một cách nhanh nhất. Chúng ta có thể hiểu qua một ví dụ sau:
Bằng cách ghép điện trở [imath]R_0[/imath] vào nguồn điện ta được một mạch điện mới với nguồn điện mới có : [imath]\left\{\begin{matrix} E=E\\ r'=r+R_0 \end{matrix}\right.[/imath]
|
|
|
Đây chỉ là một ví dụ đơn giản để ta thấy dễ hiểu và tiếp cận dễ hơn về phương pháp này, thực ra nó cũng dễ mà
Ta sẽ tổng hợp những trường hợp cơ bản nhất mà cũng dùng nhiều nhất nhé !!
Cho bài toán: Cho mạch điện như hình vẽ, các nguồn có suất điện động và điện trở trong tương ứng là [imath]\left(e_{1} ; r_{1}\right) ;\left(e_{2} ; r_{2}\right) ; \ldots .\left(e_{n} ; r_{n}\right)[/imath]. Để đơn giản, ta giả sử các nguồn có cực dương nối với [imath]A[/imath] trừ nguồn [imath]\left(e_{2} ; r_{2}\right)[/imath]. Tìm suất điện động và điện trở trong của bộ nguồn này nếu coi [imath]A[/imath] và [imath]B[/imath] là hai cực của nguồn điện tương đương.
|
H.1 |
H.2 |
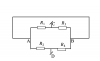
1.Nguồn địện tương đương của bộ nguồn mắc nối tiếp (H.1)
[imath]\left\{\begin{matrix} e_b=e_1-e_2+e_3+...+e_n \\ r_b=r_1+r_2+r_3+...+r_n \end{matrix}\right.[/imath]
*Đặc biệt nếu chỉ gồm điện trở [imath]R[/imath] mắc nối tiếp bộ bộ ta xem nó như một nguồn điện có [imath]e_R=0,r=R[/imath]
[imath]\Rightarrow \left\{\begin{matrix} e_b=e \\r_b=r+R \end{matrix}\right.[/imath]
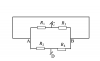
2.Nguồn điện tương đương của bộ nguồn ghép song song (H.2)
Công thức bộ nguồn như sau:[imath]\left\{\begin{matrix} \dfrac{1}{r_b}=\dfrac{1}{r_1}+\dfrac{1}{r_2}+...+\dfrac{1}{r_n}\\ \dfrac{e}{r_b}=\dfrac{e_1}{r_1}+\dfrac{e_2}{r_2}+...+\dfrac{e_n}{r_n} \end{matrix}\right.[/imath]
Chứng minh:
Giả sử cả bộ nguồn ở hình H.2 tương đương với nguồn bộ nguồn [imath](e_b;r_b)[/imath]
Gọi [imath]U_{AB}=U[/imath]Ta có định lí nút tại [imath]A[/imath] :
[imath]I=I_1-I_2+I_3+...+I_n[/imath]
[imath]\Rightarrow \dfrac{e_b-U}{r_b}=\dfrac{e_1-U}{r_1}-\dfrac{e_2+U}{r_2}+...+\dfrac{e_n-U}{r_n}[/imath]
[imath]\Rightarrow \dfrac{e_b-U}{r_b}=(\dfrac{e_1}{r_1}-\dfrac{e_2}{r_2}+...+\dfrac{e_n}{r_n})-(\dfrac{U}{r_1}+\dfrac{U}{r_2}+...+\dfrac{U}{r_n})[/imath]
Đồng nhất hệ số ta được điều cần chứng minh trên!!
*Đặc biệt nếu được mắc song song với một điện trở thuần [imath]R[/imath] khác, ta có thể quy chuẩn nó là một nguồn địên với [imath]e_R=0,r=R[/imath]
Áp dụng ngay vào một số bài toán để thấy sự hiểu quả nhé:
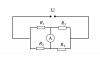
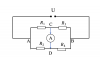
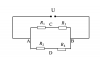
| Bài tập: Cho mạch điện như hình vẽ. Nguồn điện có suất điện động [imath]E=12V,r=1 \Omega[/imath] Điện trở [imath]R_1=5 \Omega,R_3=4 \Omega[/imath]. Tìm [imath]R_2[/imath] để công suất trên [imath]R_2[/imath] lớn nhất. |
|
Cách giải thông thường:
Ta có: [imath]I=\dfrac{ER}{r+R_{2}+\dfrac{R_{1} R_{2}}{R_{1}+R_{2}}}=\dfrac{12}{5+\dfrac{5 x}{5+x}}=\dfrac{12(5+x)}{(25+10 x)}[/imath]
Áp dụng công thức chia dòng ta được dòng qua [imath]R_{2}: I_{2}=\dfrac{R_{1}}{R_{1}+R_{2}} I=\dfrac{5}{5+x} \dfrac{12(5+x)}{(25+10 x)}=\dfrac{12}{5+2 x}[/imath]
Công suất trên [imath]R_{2}[/imath] là :
[imath]P_{2}=R_{2} I_{2}^{2}=x\left(\dfrac{12}{5+2 x}\right)^{2}=\dfrac{144 x}{(5+2 x)^{2}}=\dfrac{144 x}{(2 x-5)^{2}+40 x}=\dfrac{144}{\left(\dfrac{(2 x-5)^{2}}{x}+40\right)}[/imath]
Vậy [imath]P_{2 \max }[/imath] khi [imath]2 x=5=>x=2,5 \Omega[/imath]
Áp dụng phương pháp nguồn tương đương:
Mục tiêu biến mạch điện thành một mạch mới mà điện trở ngoài chỉ gồm [imath]R_2[/imath] và áp dụng hệ quả cực trị phụ quen thuộc:
[imath]P_{2 \max}[/imath] khi [imath]R_2=r_b[/imath] và [imath]P_{2 \max}=\dfrac{E_b^2}{4r_b}[/imath]
Các bước giải:- B1: Ghép nguồn điện [imath](E,r)[/imath] nối tiếp với nguồn [imath](0,R_3)[/imath] ta được bộ nguồn mới : [imath]\left\{\begin{matrix} E_1=E=12(V) \\ r_1=r+R_3=5(\Omega) \end{matrix}\right.[/imath]
- B2: Ghép nguồn điện [imath](E_1,r_1)[/imath] song song với nguồn [imath](0,R_1)[/imath] ta được: [imath]\left\{\begin{matrix} \dfrac{1}{r_b}=\dfrac{1}{R_1}+\dfrac{1}{r_1}=>r_b=2,5(\Omega) \\ \dfrac{E_b}{r_b}=\dfrac{E_1}{r_1}+\dfrac{0}{R_3}=>E_b=6(V) \end{matrix}\right.[/imath]
- B3: Áp dụng hệ quả : công suất trên [imath]R_2[/imath] đạt max khi [imath]R_2=r_b=2,5(\Omega)[/imath] và [imath]P_{2\max}=\dfrac{E_b^2}{4r_b}=3,6(W)[/imath]
Nếu là trắc nghiệm thì phương pháp 2 ưu việt hơn hẳn còn khi thi tự luận ở mọi bước từ công thức nguồn tương đương đến hệ quả cực trị các bạn đều phải chứng minh hết mới được áp dung nhé, đây chưa phải là những gì hay nhất về phương pháp này , hẹn các bạn ở số sau
Last edited:
