N
nhoc_maruco223
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
*Trường hợp tia phân giác và đường trung trực cắt nhau trong tam giác
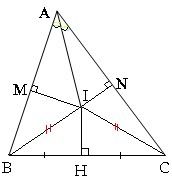
Cho tam giác ABC bất kì, Đường phân giác [tex]\hat{A}[/tex] cắt đường trung trực cạnh BC tại I.
M, N lần lượt là hình chiếu của I lên AB,AC
Xét [tex]\bigtriangleup[/tex] AIM = [tex]\bigtriangleup[/tex] AIN ( cạnh huyền góc nhọn)
=>AM=AN (1);
MI=NI (2);
Xét [tex]\bigtriangleup[/tex] BMI = [tex]\bigtriangleup[/tex] CNI ( cạnh huyền cạnh góc vuông)
=>BM=CN(3)
Từ (1) và (3)=> AM+BM=AN+CN
<=>AB=AC
Vậy [tex]\bigtriangleup[/tex] ABC cân
Vô lí
Đến đây chắc ai cũng kết luận là đường phân giác và đường trung trực cạnh đối luôn cắt nhau ngoài tam giác. Điều này có đúng không?
* Trường hợp cắt nhau ngoài tam giác
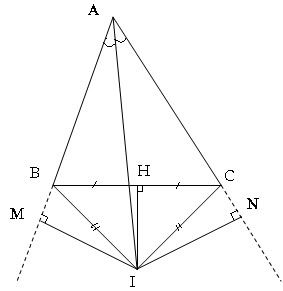
Xét [tex]\bigtriangleup[/tex] AMI = [tex]\bigtriangleup[/tex] ANI ( cạnh huyền cạnh góc nhọn)
=>MI=NI ; AM=AN (4)
Xét [tex]\bigtriangleup[/tex] BMI = [tex]\bigtriangleup[/tex] CNI ( cạnh huyền cạnh góc vuông)
=> BM = CN (5)
Từ (4) và (5) => AM-BM=AN-CN
<=>AB=AC
Vậy [tex]\bigtriangleup[/tex] ABC cân tại A.
Điều c/m " Mọi tam giác đều cân" sai ở đâu?

Cho tam giác ABC bất kì, Đường phân giác [tex]\hat{A}[/tex] cắt đường trung trực cạnh BC tại I.
M, N lần lượt là hình chiếu của I lên AB,AC
Xét [tex]\bigtriangleup[/tex] AIM = [tex]\bigtriangleup[/tex] AIN ( cạnh huyền góc nhọn)
=>AM=AN (1);
MI=NI (2);
Xét [tex]\bigtriangleup[/tex] BMI = [tex]\bigtriangleup[/tex] CNI ( cạnh huyền cạnh góc vuông)
=>BM=CN(3)
Từ (1) và (3)=> AM+BM=AN+CN
<=>AB=AC
Vậy [tex]\bigtriangleup[/tex] ABC cân
Vô lí
Đến đây chắc ai cũng kết luận là đường phân giác và đường trung trực cạnh đối luôn cắt nhau ngoài tam giác. Điều này có đúng không?
* Trường hợp cắt nhau ngoài tam giác

Xét [tex]\bigtriangleup[/tex] AMI = [tex]\bigtriangleup[/tex] ANI ( cạnh huyền cạnh góc nhọn)
=>MI=NI ; AM=AN (4)
Xét [tex]\bigtriangleup[/tex] BMI = [tex]\bigtriangleup[/tex] CNI ( cạnh huyền cạnh góc vuông)
=> BM = CN (5)
Từ (4) và (5) => AM-BM=AN-CN
<=>AB=AC
Vậy [tex]\bigtriangleup[/tex] ABC cân tại A.
Điều c/m " Mọi tam giác đều cân" sai ở đâu?

