- 28 Tháng một 2016
- 3,897
- 1
- 8,081
- 939
- Yên Bái
- THPT Lê Quý Đôn <3
Chúc cả nhà buổi tối an lành, nay mình chuyển sang 1 chút quang học cho cân bằng nội dung nha 
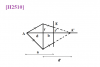
[H2510] Một điểm sáng $A$ đặt trước màn $E$ một khoảng $a=50cm$. Trong khoảng cách giữa $A$ và $E$ người ta đặt một thấu kính $L$ sao cho $A$ nằm trên trục chính và $L$ song song với E. Khi tịnh tiến thấu kính theo trục chính trong khoảng cách giữa $A$ và $E$ người ta thấy vệt sáng trên màn không bao giờ thu lại thành một điểm nhưng khi $L$ cách $E$ một khoảng $b=20cm$ thì vệt sáng trên màn có bán kính nhỏ nhất. Tính tiêu cự của thấu kính $L$
[H2510] Một điểm sáng $A$ đặt trước màn $E$ một khoảng $a=50cm$. Trong khoảng cách giữa $A$ và $E$ người ta đặt một thấu kính $L$ sao cho $A$ nằm trên trục chính và $L$ song song với E. Khi tịnh tiến thấu kính theo trục chính trong khoảng cách giữa $A$ và $E$ người ta thấy vệt sáng trên màn không bao giờ thu lại thành một điểm nhưng khi $L$ cách $E$ một khoảng $b=20cm$ thì vệt sáng trên màn có bán kính nhỏ nhất. Tính tiêu cự của thấu kính $L$





 Chúc các bạn may mắn ^^
Chúc các bạn may mắn ^^