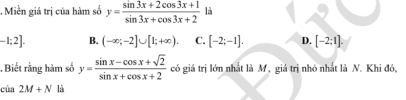[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Miền giá trị của hàm số [imath]y=\dfrac{\sin 3x+2\cos 3x+1}{\sin 3x+\cos 3x+2}[/imath]
Câu này hộ hỏi tìm miền giá trị thì làm saoạ?em không hiểu rỗ miền giá trị so với tập xácđịnhýạ. bài này thì e kh hiểu vì sào mẫu luôn lớn hơn 0ạ
Câu này hộ hỏi tìm miền giá trị thì làm saoạ?em không hiểu rỗ miền giá trị so với tập xácđịnhýạ. bài này thì e kh hiểu vì sào mẫu luôn lớn hơn 0ạ
Attachments
Last edited by a moderator: