- 19 Tháng tám 2018
- 2,749
- 6,038
- 596
- 25
- Thái Bình
- Đại học Y Dược Thái Bình
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Hôm nay mình đến với một dạng toán mới của lượng giác nhé, đó là hệ thức lượng trong tam giác. Trước tiên để giải được những bài toán về hệ thức lượng trong tam giác cũng như các bài toán định dạng tam giác ta cần biết các kiến thức sau:
1. Hệ thức hàm số cosin:

[imath]\qquad \qquad \qquad \begin{aligned} a^2 & = b^2 + c^2 - 2bc \cos A \\ b^2 & = a^2 + c^2 - 2ac \cos B \\ c^2 & = a^2 + b^2 - 2ab \cos C \end{aligned}[/imath]
2. Hệ thức hàm số sin:
[imath]\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R[/imath] (trong đó: [imath]R[/imath] là bán kính đường tròn ngoại tiếp tam giác )
3. Hệ thức đường trung tuyến:
 [imath]\qquad \qquad \qquad \qquad \begin{aligned} b^2 + c^2 & = 2m_a^2 + \dfrac{a^2}2 \\ a^2 + c^2 & = 2m_b^2 + \dfrac{b^2}2 \\ a^2 + b^2 & = 2m_c^2 + \dfrac{c^2}2 \end{aligned}[/imath]
[imath]\qquad \qquad \qquad \qquad \begin{aligned} b^2 + c^2 & = 2m_a^2 + \dfrac{a^2}2 \\ a^2 + c^2 & = 2m_b^2 + \dfrac{b^2}2 \\ a^2 + b^2 & = 2m_c^2 + \dfrac{c^2}2 \end{aligned}[/imath]
4. Hệ thức đường phân giác :
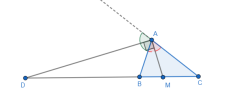
[imath]\dfrac{MB}{MC} = \dfrac{NB}{NC} = \dfrac{AB}{AC}[/imath]
Trong đó: [imath]AM, AN[/imath] lần lượt là các đường phân giác trong và ngoài của góc [imath]A[/imath]
5. Hệ thức đường cao:

[imath]AB^2 - AC^2 = 2 BC \cdot OH[/imath]
Trong đó: [imath]AH[/imath] là đường cao, [imath]O[/imath] là trung điểm của [imath]BC[/imath]
6. Diện tích tam giác:
[imath]S = \dfrac{1}2bc \sin A = \dfrac{1}2 ac\sin B = \dfrac{1}2 ab \sin C[/imath]
[imath]S = pr[/imath] ( với [imath]p[/imath]: nửa chu vi, [imath]r[/imath]: bán kính đường tròn nội tiếp tam giác )
[imath]S = \dfrac{abc}{4R}[/imath] ( với [imath]R[/imath] là bán kính đường tròn ngoại tiếp tam giác)
7. Một số công thức khác:
[imath]\sin A + \sin B + \sin C = 4\cos \dfrac{A}2 \cos \dfrac{B}2 \cos \dfrac{C}2[/imath]
[imath]\cos A + \cos B + \cos C = 4\sin \dfrac{A}2 \sin \dfrac{B}2 \dfrac{C}2 + 1[/imath]
[imath]\sin^2 A + \sin^2B + \sin^2 C = 2\cos A \cos B \cos C + 2[/imath]
[imath]\tan A + \tan B + \tan C = \tan A \tan B \tan C \qquad \left( A,B,C \ne \dfrac{\pi}2 \right)[/imath]
[imath]\cot \dfrac{A}2 + \cot \dfrac{B}2 + \cot \dfrac{C}2 = \cot \dfrac{A}2 \cdot \dfrac{B}2 \cdot \dfrac{C}2[/imath]
[imath]\cot A \cot B + \cot A \cot C + \cot B \cot C = 1[/imath]
[imath]\sin 2A + \sin 2B + \sin 2C = 4\sin A \sin B \sin C[/imath]
Phần bài tập mình sẽ cập nhật ở những bài tiếp theo. Mọi người nhớ theo dõi nhé ^^
_________________________________
Xem thêm: [Lượng giác] Chứng minh đẳng thức lượng giác
1. Hệ thức hàm số cosin:
Tam giác [imath]ABC[/imath] với [imath]BC = a,\, AC = b, \, AB = c[/imath] thì:
[imath]\qquad \qquad \qquad \begin{aligned} a^2 & = b^2 + c^2 - 2bc \cos A \\ b^2 & = a^2 + c^2 - 2ac \cos B \\ c^2 & = a^2 + b^2 - 2ab \cos C \end{aligned}[/imath]
2. Hệ thức hàm số sin:
[imath]\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R[/imath] (trong đó: [imath]R[/imath] là bán kính đường tròn ngoại tiếp tam giác )
3. Hệ thức đường trung tuyến:
 [imath]\qquad \qquad \qquad \qquad \begin{aligned} b^2 + c^2 & = 2m_a^2 + \dfrac{a^2}2 \\ a^2 + c^2 & = 2m_b^2 + \dfrac{b^2}2 \\ a^2 + b^2 & = 2m_c^2 + \dfrac{c^2}2 \end{aligned}[/imath]
[imath]\qquad \qquad \qquad \qquad \begin{aligned} b^2 + c^2 & = 2m_a^2 + \dfrac{a^2}2 \\ a^2 + c^2 & = 2m_b^2 + \dfrac{b^2}2 \\ a^2 + b^2 & = 2m_c^2 + \dfrac{c^2}2 \end{aligned}[/imath]4. Hệ thức đường phân giác :

[imath]\dfrac{MB}{MC} = \dfrac{NB}{NC} = \dfrac{AB}{AC}[/imath]
Trong đó: [imath]AM, AN[/imath] lần lượt là các đường phân giác trong và ngoài của góc [imath]A[/imath]
5. Hệ thức đường cao:

[imath]AB^2 - AC^2 = 2 BC \cdot OH[/imath]
Trong đó: [imath]AH[/imath] là đường cao, [imath]O[/imath] là trung điểm của [imath]BC[/imath]
6. Diện tích tam giác:
[imath]S = \dfrac{1}2bc \sin A = \dfrac{1}2 ac\sin B = \dfrac{1}2 ab \sin C[/imath]
[imath]S = pr[/imath] ( với [imath]p[/imath]: nửa chu vi, [imath]r[/imath]: bán kính đường tròn nội tiếp tam giác )
[imath]S = \dfrac{abc}{4R}[/imath] ( với [imath]R[/imath] là bán kính đường tròn ngoại tiếp tam giác)
7. Một số công thức khác:
[imath]\sin A + \sin B + \sin C = 4\cos \dfrac{A}2 \cos \dfrac{B}2 \cos \dfrac{C}2[/imath]
[imath]\cos A + \cos B + \cos C = 4\sin \dfrac{A}2 \sin \dfrac{B}2 \dfrac{C}2 + 1[/imath]
[imath]\sin^2 A + \sin^2B + \sin^2 C = 2\cos A \cos B \cos C + 2[/imath]
[imath]\tan A + \tan B + \tan C = \tan A \tan B \tan C \qquad \left( A,B,C \ne \dfrac{\pi}2 \right)[/imath]
[imath]\cot \dfrac{A}2 + \cot \dfrac{B}2 + \cot \dfrac{C}2 = \cot \dfrac{A}2 \cdot \dfrac{B}2 \cdot \dfrac{C}2[/imath]
[imath]\cot A \cot B + \cot A \cot C + \cot B \cot C = 1[/imath]
[imath]\sin 2A + \sin 2B + \sin 2C = 4\sin A \sin B \sin C[/imath]
Phần bài tập mình sẽ cập nhật ở những bài tiếp theo. Mọi người nhớ theo dõi nhé ^^
_________________________________
Xem thêm: [Lượng giác] Chứng minh đẳng thức lượng giác