 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cho (O) và A nằm ngoài đường tròn. Vẽ tiếp tuyến AB và AC , cát tuyến ADE không đi qua tâm O .Gọi H là trung điểm của DE , I là giao điểm BC và DE .
a, CM ABOC nội tiếp. Xác định tâm
b, CM HA là phân giác BHC
c, AI.AH=AD.AE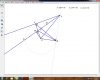
a, CM ABOC nội tiếp. Xác định tâm
b, CM HA là phân giác BHC
c, AI.AH=AD.AE

Last edited:

