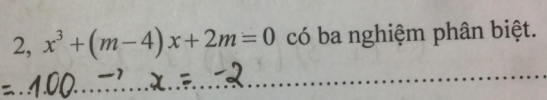@Thiên An - 2009 Trong trường hợp bạn thấy lời giải trên magic quá, ko rõ công thức từ đâu thì bạn có thể làm các bước sau:
Đầu tiên, chấp tay cầu nguyện đây thực sự là toán lớp 9, phương trình sẽ có tính chất đặc biệt gì đó, chứ không cần phải xài tới phương pháp lớp 12 hay nhớ công thức bậc 3 (mình quên mất công thức nên gì rồi, Cardano gì à

)
Tiếp theo, tách [imath]m[/imath] qua một bên: [math]m(x + 2) = -x^3 + 4x = -x(x - 2)(x + 2)[/math]
Ohhhhh, [imath]x = -2[/imath] là một nghiệm nè. Phần còn lại: [math]m = -x(x - 2)[/math]
Để phương trình có 3 nghiệm phân biệt thì phương trình [imath]x^2 - 2x + m = 0[/imath] trên phải có 2 nghiệm phân biệt khác [imath]-2[/imath]
Tới đây dễ rồi: đầu tiên là 2 nghiệm phân biệt thì [imath]\Delta' = 1 - m > 0[/imath] hay [imath]m < 1[/imath]
Rồi để hai nghiệm khác [imath]-2[/imath] thì [imath](-2)^2 - 2 \cdot (-2) + m \ne 0[/imath] hay [imath]m \ne -8[/imath].
Vậy [imath]m < 1[/imath] và [imath]m \ne -8[/imath] nhé.
Womp womp, vậy là
@ngia sai ở đâu gòi. Đây là cái giá của công thức ma thuật khi bạn không rõ công thức từ đâu ra hết

 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.