Hình như đề thiếu [imath]a\in [-1,1][/imath] em nhỉ
Xét [imath]a=1\Rightarrow m=31[/imath] (thỏa)
Xét [imath]a\in [-1,1)[/imath]
pt [imath]\Leftrightarrow \dfrac{7a-m+24}{a^2-3a+2}=\sqrt{2a^3+a^2+m-9}[/imath] (1)
Đk cần là [imath]7a-m+24\ge 0\Rightarrow 31-m>0\Rightarrow 31>m[/imath] (1)
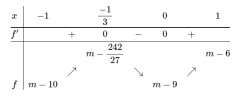
[imath]2a^3+a^2+m-9\ge 0\Rightarrow m-6\ge 0\Rightarrow m\ge 6[/imath]
với [imath]a\in [-1,1)[/imath] thì [imath]a^2-3a+2[/imath] nghịch biến; [imath]7a-m+24[/imath] đồng biến
[imath]\Rightarrow \dfrac{7a-m+24}{a^2-3a+2}[/imath] đồng biến; [imath]\dfrac{7a-m+24}{a^2-3a+2}\in [\dfrac{17-m}6, +\infty)[/imath]
Đặt [imath]f(x)=2a^3+a^2+m-9[/imath]
View attachment 215368
Đk cần để (1) có nghiệm là
[imath]max \sqrt{f(x)}\ge min \dfrac{7a-m+24}{a^2-3a+2}[/imath]
[imath]\Rightarrow \sqrt{m-6}\ge \dfrac{17-m}6\Rightarrow m\ge 9[/imath] (2)
Từ (1) (2) ta có: [imath]31>m\ge 9[/imath]
Ta có: [imath]\sqrt{m-10}\ge \dfrac{17-m}6[/imath]
[imath]\Leftrightarrow 59\ge m\ge 11[/imath]
TH1: [imath]31>m\ge 11[/imath] thì đồ thị hai hàm số như sau nên (1) có nghiệm
View attachment 215369
TH2: [imath]m=10[/imath] hoặc [imath]m=9[/imath] em vẽ đồ thị tương giao ra sẽ thấy nó không có nghiệm
Có gì khúc mắc em hỏi lại nha
Ngoài ra, em xem thêm tại
Hàm số lượng giác và phương trình lượng giác
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.