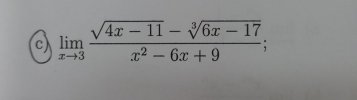Tính giới hạn hàm số sau
[imath]\lim_{x \to 3} \dfrac{\sqrt{4x -11} - \sqrt[3]{6x -17}}{x^2 -6x +9}[/imath]
Joli Talentueux
[imath]\lim_{x \to 3} \dfrac{\sqrt{4x -11} - \sqrt[3]{6x -17}}{x^2 -6x +9}[/imath]
[imath]= \lim_{x \to 3} \dfrac{(\sqrt{4x -11} -1) + (1 - \sqrt[3]{6x -17})}{x^2 -6x +9}[/imath]
[imath]= \lim_{x \to 3} \dfrac{\dfrac{4(x -3)}{\sqrt{4x -11} +1}- \dfrac{6(x-3)}{\sqrt[3]{6x -17}^2 + \sqrt[3]{6x -17} +1}}{x^2 -6x +9}[/imath]
[imath]= \lim_{x \to 3} \dfrac{\dfrac{4}{\sqrt{4x -11} +1}- \dfrac{6}{\sqrt[3]{6x -17}^2 + \sqrt[3]{6x -17} +1}}{x - 3}[/imath]
[imath]= \lim_{x \to 3} \dfrac{\left (\dfrac{4}{\sqrt{4x -11} +1} - 2 \right) + \left (2 - \dfrac{6}{\sqrt[3]{6x -17}^2 + \sqrt[3]{6x -17} +1} \right)}{x - 3}[/imath]
( Đặt [imath]\sqrt[3]{6x - 17} = A[/imath]
[imath]= \lim_{x \to 3} \dfrac{\dfrac{2- 2\sqrt{4x -11}}{\sqrt{4x -11} +1} + \dfrac{2A^2 +2A - 6}{A^2 +A +1}}{x - 3}[/imath]
[imath]= \lim_{x \to 3} \dfrac{-8}{(\sqrt{4x -11} +1)^2} + \dfrac{12(A+2)}{(A^2 +A +1)^2}[/imath]
[imath]= \dfrac{-8}{4} + \dfrac{36}{9} = 2[/imath]
Có gì không hiểu thì em hỏi lại nha
Ngoài ra, em tham khảo thêm kiến thức tại
Tổng hợp kiến thức toán 11
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
