- 29 Tháng bảy 2018
- 581
- 972
- 126
- TP Hồ Chí Minh
- THPT Đức Linh - Bình Thuận
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
CHỦ ĐỀ: HÌNH HỌC PHẲNG TRONG GIAO THOA SÓNG CƠ
I. Lời nói đầuMột trong những dạng bài tập xếp vào loại khó trong Giao thoa sóng cơ, đó là tìm số cực đại hoặc cực tiểu trên một đoạn thẳng bất kỳ, có thể là trên một cạnh của hình chữ nhật, cạnh của một tam giác hay đường tròn...
Về hướng giải quyết dạng bài toán này thì thực ra không khó, chỉ có một cách duy nhất đó là tìm giới hạn trên và giới hạn dưới của bậc [tex]k[/tex] tại hai đầu nút, dựa vào công thức hiệu đường đi [tex]d_2-d_1=k\lambda[/tex]
II. Lý thuyết
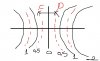
1. Hình vẽ minh họa mẫu

- Nếu đề bài yêu cầu tính số cực đại hay cực tiểu trên đoạn [tex]CD[/tex] thì ta tìm hai bậc tại hai điểm [tex]C, D[/tex] từ công thức hiệu đường đi. Cụ thể như sau:
+ Ta chọn nguồn [tex]A[/tex] là nguồn [tex]1[/tex], nguồn [tex]B[/tex] là nguồn [tex]2[/tex]
+ Điểm [tex]C[/tex]: [tex]d_2-d_1=k_C \lambda<=>BC-AC=k_C \lambda[/tex], ta tính được [tex]k_C[/tex]
+ Điểm [tex]D[/tex]: [tex]d_2-d_1=k_D \lambda<=>DB-DA=k_D \lambda[/tex], ta tính được [tex]k_D[/tex]
* Số cực đại trên đoạn [tex]CD[/tex] thì tương ứng với giá trị [tex]k[/tex] là số nguyên thỏa mãn:
[tex]k_C\leq k\leq k_D[/tex]
* Số cực tiểu trên đoạn [tex]CD[/tex] thì tương ứng với giá trị [tex]k[/tex] là số bán nguyên thỏa mãn:
[tex]k_C\leq k\leq k_D[/tex]
2. Bài tập mẫu:
Đề bài: Trên mặt thoáng chất lỏng, hai nguồn sóng kết hợp [tex]S_1,S_2[/tex] cùng pha, cùng tần số [tex]f=10(Hz)[/tex]. Tốc độ truyền sóng trên mặt nước là [tex]24(cm/s)[/tex]. Khoảng cách hai nguồn [tex]S_1,S_2[/tex]là [tex]12(cm)[/tex]. Xét hai điểm [tex]A, B[/tex] trên mặt thoáng chất lỏng sao cho [tex]S_1ABS_2[/tex] là hình chữ nhật có diện tích [tex]60(cm^2)[/tex]
a) Tính số điểm dao động cực đại, cực tiểu trên đoạn thẳng nối hai nguồn [tex]S_1,S_2[/tex]
b) Tính số điểm dao động cực đại trên đoạn [tex]AB[/tex]
c) Tính số điểm dao động cực tiểu trên đoạn [tex]AB[/tex]
GIẢI:

* Bước sóng [tex]\lambda = \frac{v}{f}=2,4(cm)[/tex]
a) Để làm câu này, thì các em tham khảo bài viết này: CỰC ĐẠI, CỰC TIỂU TRÊN ĐOẠN THẲNG NỐI HAI NGUỒN
b) Để tính số điểm cực đại, cực tiểu trên đoạn [tex]AB[/tex] thì ta tính bậc tại [tex]A[/tex] và [tex]B[/tex]
* Vì diện tích hình chữ nhật là [tex]60(cm^2)[/tex], mà [tex]S_1S_2=12(cm)[/tex] nên ta tính được [tex]AS_1=BS_2=5(cm)[/tex]
Từ đó, áp dụng Py - ta - go ta tính được [tex]AS_2=13(cm);BS_1=13(cm)[/tex]
- Ta tính bậc tại [tex]A[/tex]: [tex]k_A=\frac{d_2-d_1}{\lambda}=\frac{AS_2-AS_1}{\lambda}=\frac{13-5}{2,4}=3,3[/tex]
- Ta tính bậc tại [tex]B[/tex]: [tex]k_B=\frac{d_2-d_1}{\lambda}=\frac{BS_2-BS_1}{\lambda}=\frac{5-13}{2,4}=-3,3[/tex]
* Vậy, số cực đại trên đoạn [tex]AB[/tex] thỏa mãn giá trị nguyên của [tex]k[/tex] như sau
[tex]k_B\leq k\leq k_A<=>-3,3\leq k\leq 3,3[/tex]
Ta đếm được có [tex]07[/tex] giá trị thỏa mãn => trên đoạn [tex]AB[/tex] có [tex]07[/tex] điểm cực đại
c) Ta sử dụng luôn kết quả của câu [tex]b)[/tex] để tìm số điểm cực tiểu trên [tex]AB[/tex], trong đó giá trị [tex]k[/tex] là số bán nguyên thỏa mãn
[tex]k_B\leq k\leqslant k_A<=>-3,3\leqslant k\leqslant k_A[/tex] , vậy có các giá trị bán nguyên[tex](-2,5);(-1,5);(-0,5);(0,5);(1,5)(2,5)[/tex] thỏa mãn => có [tex]06[/tex] điểm cực tiểu trên đọan [tex]AB[/tex]
III. Bài tập vận dụng
Bài 01: Giao thoa sóng ở mặt nước với hai nguồn kết hợp đặt tại A và B. Hai nguồn dao động điều hòa theo phương thẳng đứng, cùng pha, cùng tần số [tex]10(Hz)[/tex]. Biết [tex]AB=20(cm)[/tex], tốc độ truyền sóng trên mặt nước là [tex]0,3(m/s)[/tex]. Ở mặt nước, gọi [tex]\Delta[/tex] là đường thẳng đi qua trung điểm của AB và hợp với AB góc [tex]60^0[/tex]. Trên [tex]\Delta[/tex] có bao nhiêu điểm mà phần tử ở đó dao động với biên độ cực đại?
A. 11 điểm
B. 07 điểm
C. 13 điểm
D. 09 điểm
Bài 02: Trong hiện tượng giao thoa sóng trên mặt nước, hai nguồn sóng kết hợp cùng pha, cùng tần số [tex]25(Hz)[/tex] được đặt taị hai điểm A và B cách nhau [tex]10(cm)[/tex]. Tốc độ truyền sóng trên mặt nước là [tex]40(cm/s)[/tex]. Kẻ đường thẳng [tex]By[/tex] trên mặt nước sao cho [tex]By[/tex] và [tex]AB[/tex] vuông góc. Gọi [tex]M[/tex] thuộc [tex]By[/tex] dao động với biên độ cực đại. Khoảng cách lớn nhất từ [tex]M[/tex] đến [tex]B[/tex] bằng?
A. [tex]32,05(cm)[/tex]
B. [tex]30,45(cm)[/tex]
C. [tex]0,41(cm)[/tex]
D. [tex]10,01(cm)[/tex]
Bài 03: Tại hai điểm A, B trên mặt nước, đặt hai nguồn sóng kết hợp dao động cùng pha, cùng tần số [tex]20(Hz)[/tex], dao động theo phương vuông góc với mặt nước. Biết [tex]AB=8,0(cm)[/tex], tốc độ truyền sóng trên mặt nước là [tex]30(cm/s)[/tex]. Xét đoạn thẳng [tex]CD=4,0(cm[/tex] trên mặt nước có chung đường trung trực với đoạn thằng [tex]AB[/tex]. Tính khoảng cách lớn nhất từ [tex]CD[/tex] đến [tex]AB[/tex] sao cho trên đoạn [tex]CD[/tex] chỉ có [tex]03[/tex] điểm dao động với biên độ cực đại.
A. [tex]3,3(cm)[/tex]
B. [tex]6,0(cm)[/tex]
C. [tex]8,9(cm)[/tex]
D. [tex]9,7(cm)[/tex]
----------------------------------------------------------------HẾT-------------------------------------------------------
Chúc các em hoàn thành tốt !