Giải pt nghiệm nguyên: [tex]3x-16y-24=\sqrt{9x^{2}+16x+32}[/tex]
x.y nguyên=> 3x-16y-24 nguyên => [tex]\sqrt{9x^2+16x+32}[/tex] nguyên
gọi [tex]a[/tex]([tex]a\in N[/tex]) là 1 giá trị của [tex]\sqrt{9x^2+16x+32}[/tex] , pt [tex]\sqrt{9x^2+16x+32}=a[/tex] có nghiệm =>[tex]9x^2+16x+32-a^2=0[/tex] có nghiệm
<=> [tex]\Delta '\geq 0\Leftrightarrow -224+9a^2\geq 0\Rightarrow a\geq \frac{4\sqrt{14}}{3}[/tex]
mà [tex]a\in N[/tex]
=> [tex]a>\frac{4\sqrt{14}}{3}[/tex]
để [tex]9x^2+16x+32-a^2=0[/tex] có nghiệm x nguyên thì [tex]\Delta '=-224+9a^2[/tex] phải là số chính phương
đặt [tex]-224+9a^2=b^2(b\in N)[/tex]
<=> (3a-b)(3a+b)=224 (1)
ta có 3a-b và 3a+b có cùng tính chẵn lẻ (2)
ta lại có [tex]a\in N;b\in N[/tex] [tex]\Rightarrow 3a+b\geq 3a-b[/tex] (3)
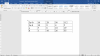
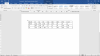
từ (1),(2) và (3) ta có bảng sau :
(hình gửi kèm)
...............................................................................................................................................................................................................................................
=> (x;y)=(-1;-2),(-7;-4)
bạn kt lại giúp mình nha!
cách làm của mình chưa dc hay lắm mong bạn góp ý thêm
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.