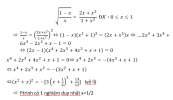Em tham khảo thêm cách này nha
_________
đk [imath]0< x\le 1[/imath]
[imath]\sqrt{\dfrac{1-x}{x}}=\dfrac{2x+x^2}{1+x^2}\Leftrightarrow \sqrt{\dfrac{1-x}{x}}=\dfrac{2x-1}{1+x^2}+1[/imath]
[imath]\Leftrightarrow \sqrt{\dfrac{1-x}{x}}-1=\dfrac{2x-1}{1+x^2}\Leftrightarrow \dfrac{\sqrt{1-x}-\sqrt{x}}{\sqrt{x}}=\dfrac{2x-1}{1+x^2}[/imath]
[imath]\Leftrightarrow \dfrac{1-2x}{\sqrt{x}(\sqrt{1-x}+\sqrt{x})}=\dfrac{2x-1}{1+x^2}[/imath]
[imath]\Leftrightarrow (2x-1)\left(\dfrac{1}{\sqrt{x}(\sqrt{1-x}+\sqrt{x})}+\dfrac{1}{x^2+1}\right)=0[/imath]
[imath]\Leftrightarrow x=\dfrac{1}2[/imath] ( do [imath]\dfrac{1}{\sqrt{x}(\sqrt{1-x}+\sqrt{x})}+\dfrac{1}{x^2+1}>0 \forall\: x\in (0,1][/imath])
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em xem thêm tại
[Bài tập] Chuyên đề HSG: Phương trình vô tỷ
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.