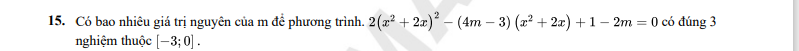Đặt [imath]x^2 + 2x = t[/imath]
[imath]
\begin{array}{c|ccccc}
x & -3 & & -1 & & 0 \\
\hline
y' & & + & 0 & - & \\
\hline
y & 3 & & & & 0 \\
& & \searrow & & \nearrow & \\
& & & -1 & &
\end{array}[/imath]
Cứ 1 giá trị [imath]t[/imath] thì có [imath]0;1;2[/imath] nghiệm [imath]x[/imath]
Phương trình [imath]\iff 2t^2 -(4m-3)t +1-2m = 0 (1)[/imath]
Để phương trình có đúng 3 nghiệm thì (1) có 2 nghiệm [imath]t[/imath] thỏa mãn
TH1: [imath]t_1 = -1[/imath] và [imath]-1 <t_2 \le 0[/imath]
Thay nghiệm [imath]t_1 = -1[/imath] vào phương trình có: [imath]2 +4m - 3 + 1 -2m = 0 \iff m = 0[/imath]
Thử lại: Thay [imath]m = 0[/imath] vào (1) xem [imath]t_2[/imath] có thỏa mãn đk hay không
TH2: [imath]-1 <t_1 \le 0 < t_2 \le 3[/imath]
1) [imath]t_1 = 0[/imath]. Tương tự TH1
2) [imath]t_2 = 3[/imath]
2) [imath]-1 <t_1 <0 <t_2 < 3[/imath]
[imath]\left\{\begin{matrix}af(0) <0 \\ af(-1) > 0 \\ af(3) > 0\\ -2 < S < 6 \end{matrix}\right.\iff \left\{\begin{matrix}1 -2m <0 \\ 2 +4m -3 +1-2m >0 \\18 -3(4m -3) +1 -2m >0 \\ -2 < \dfrac{4m -3}{2} < 6 \end{matrix}\right. \iff \left\{\begin{matrix}m > \dfrac{1}{2} \\ m > 0 \\ m <2 \\ \dfrac{-1}{4} < m < \dfrac{15}{4} \end{matrix}\right. \iff 0 < m < 2[/imath]
Có gì không hiểu thì em hỏi lại nha
Ngoài ra, em tham khảo kiến thức tại topic này nha
Xin chào tất cả các bạn thành viên diễn đàn HOCMAI - Cộng đồng Học sinh Việt Nam Chào mừng các bạn đến với THIÊN ĐƯỜNG KIẾN THỨC trên diễn đàn HOCMAI. Tại đây, diễn đàn sẽ tổng hợp tất cả các nội dung kiến thức từ cơ bản đến nâng cao, từ lý thuyết đến thực tiễn, đề thi,... của các môn Toán, Ngữ...
diendan.hocmai.vn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
