Câu 1:
a) Thời gian nêm đi được một đoạn a là:
[tex]t=\frac{s_2}{v_2}=\frac{a}{v_2}=\frac{h_0}{4v_2}[/tex]
Trong thời gian này nhện đã đi được quãng đường:
[tex]s_1=v_1t=\frac{h_0.v_1}{4v_2}[/tex] (1)
Mặt khác, lúc đó N,A,B thẳng hàng và NA=AB nên quãng đường nhện đi được trong thời gian t là:
[tex]s_1=h_0-(AN+AB)=h_0-(\frac{h_0}{4}+\frac{h_0}{4})=\frac{h_0}{2}[/tex] (2)
Từ (1) và (2) suy ra:
[tex]\frac{h_0}{2}=\frac{h_0.v_1}{4v_2}\Rightarrow \frac{v_1}{v_2}=2[/tex] (3)
b)
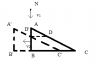
Gọi D' là vị trí nhện chạm mặt nên AC. Lúc đó cái nêm ở vị trí A'B'C'. D là vị trí của D' lúc N,A,B thẳng hàng.
Sau thời gian t'=4s, cái nêm đi được:
[tex]DD'=s_2'=v_2.t'[/tex]
[tex]\Rightarrow AD'=DD'.tan\alpha=v_2t'.tan\alpha[/tex]
Quãng đường mà con nhện đi được trong thời gian đó là:
[tex]s_1'=NA+AD'=\frac{h_0}{2}+v_2t'.tan\alpha=\frac{4a}{2}+v_2t'.tan\alpha=2a+v_2t'.tan\alpha[/tex]
Mà [tex]s_1'=v_1t'[/tex]
Do đó: [tex]v_1t'=2a+v_2t'.tan\alpha[/tex] (4)
Từ (3) và (4) suy ra:
[tex]v_2=\frac{2a}{t'(2-tan\alpha)}=\frac{2.0,8}{4(2-tan30)}=\frac{12+2\sqrt{3}}{55}\approx 0,28(m/s)[/tex]
[tex]\Rightarrow v_1=2v_2=0,56(m/s)[/tex]
Câu 2:
a)
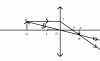
Ta có: [tex]\Delta OAB\sim \Delta OA'B'[/tex]
[tex]\Rightarrow \frac{A'B'}{AB}=\frac{OA'}{OA}[/tex] (1)
[tex]\Delta OF'I\sim \Delta A'F'B'[/tex]
[tex]\Rightarrow \frac{A'B'}{OI}=\frac{AF'}{OF'}=\frac{OA'-OF'}{OF'}[/tex] (2)
Mà OI=AB nên từ (1) và (2) suy ra:
[tex]\frac{OA'}{OA}=\frac{OA'-OF'}{OF}\Rightarrow OA'=\frac{OA.OF}{OA-OF}[/tex] (3)
Mặt khác (1)[tex]\Rightarrow OA'=\frac{A'B'.OA}{AB}[/tex] (4)
Từ (3) và (4) suy ra:
[tex]\frac{A'B'.OA}{AB}=\frac{OA.OF}{OA-OF}\Rightarrow \frac{A'B'}{AB}=\frac{OF}{OA-OF}\Rightarrow \frac{A'B'}{AB}=\frac{OF}{OA-OF}[/tex]
Hay [tex]\frac{h}{h'}=\frac{f}{d-f}[/tex]
b) Vật ở M, ta có:
[tex]\frac{h_1}{h}=\frac{f}{d_1-f}\Rightarrow d_1=f(\frac{h}{h_1}+1)[/tex]
Vật ở I, ta có:
[tex]\frac{h_2}{h}=\frac{f}{d_2-f}\Rightarrow d_2=f(\frac{h}{h_2}+1)[/tex]
Vật ở N, ta có:
[tex]\frac{h_3}{h}=\frac{f}{d_3-f}\Rightarrow d_3=f(\frac{h}{h_3}+1)[/tex]
Vì I là trung điểm MN nên:
[tex]d_2=\frac{d_1+d_3}{2}\Rightarrow f(\frac{h}{h_2}+1)=f(\frac{h(\frac{1}{h_1}+\frac{1}{h_3})+2}{2})\Rightarrow \frac{h}{h_2}+1=\frac{h(h_1+h_3)}{2h_1h_3}+1[/tex]
[tex]\Rightarrow h_2=\frac{2h_1h_3}{h_1+h_3}=\frac{2.\frac{4}{3}.4}{\frac{4}{3}+4}=2(cm)[/tex]
Câu 3:
a)*Bỏ cục nước đá vào:
Đá không tan hết [tex]\Rightarrow[/tex] nhiệt độ lúc cân bằng là [tex]t'=0^0C[/tex]
Theo đề ra, thể tích còn lại của cục nước đá là: [tex]V''=\frac{60}{100}V\Rightarrow \frac{V''}{V}=\frac{3}{5}\Rightarrow \frac{m''}{m}=\frac{3}{5}\Rightarrow m''=0,6m[/tex]
Phương trình cân bằng nhiệt lần 1:
[tex]\lambda .(m-m'')=10.(mc+MC)\Rightarrow MC=\frac{\lambda .0,4m-10mc}{10}[/tex]
Với M và C là khối lượng và nhiệt dung riêng của bình
* Đổ thêm nước vào:
Xét lượng nước và cục đá ban đầu: cột nước có độ cao h. Vì bỏ qua sự dãn nở vì nhiệt của nước thì sau khi cục nước đá tan hết lượng nước trong cốc vẫn ở độ cao h
[tex]\Rightarrow[/tex] Lượng nước đổ thêm vào có độ cao 2h
Ta có: [tex]\frac{m'}{2m}=\frac{2h}{h}=2\Rightarrow \frac{m'}{m}=4[/tex]
b) Nhiệt lượng cần để cục nước đá còn lại tan hết là:
[tex]Q_1=\lambda .m''=0,6m.\lambda [/tex]
Nhiệt lượng cần để bình và nước trong bình tăng đến nhiệt độ t là:
[tex]Q_2=MCt+2mct=\frac{\lambda .0,4m-10mc}{10}t+2mct[/tex]
Nhiệt lượng cần để lượng nước đổ vào giảm xuống nhiệt độ t:
[tex]Q=m'c(20-t))=4mc(20-t)[/tex]
Phương trình cân bằng nhiệt:
[tex]Q=Q_1+Q_2\Leftrightarrow 4mc(20-t)=0,6m.\lambda +\frac{\lambda .0,4m-10mc}{10}t+2mct[/tex]
[tex]\Rightarrow t=\frac{800c-6\lambda }{50c+0,4\lambda }=\frac{800.4200-6.3,4.10^5}{50.4200+0,4.3,4.10^5}\approx 3,82^0C[/tex]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

