- 20 Tháng chín 2013
- 5,018
- 7,484
- 941
- TP Hồ Chí Minh
- Đại học Bách Khoa TPHCM
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 1. (4 điểm)
Cho $x, y$ là các số thực sao cho $\dfrac{2}x - \dfrac{1}y = \dfrac{1}{2x+y}$. Tính giá trị của biểu thức $\dfrac{x^2}{y^2} + \dfrac{y^2}{x^2}$.
Bài 2. (3 điểm)
Cho $a, b, c$ là ba số thực sao cho $a+b = c-2$ và $ab = 2c^2-3c+1$. Tìm giá trị lớn nhất của biểu thức $P = a^2+b^2$.
Bài 3. (3 điểm)
An khởi hành từ Sài Gòn đi Biên Hòa. Sau đó 5 phút, Bình và Cường khởi hành từ Biên Hòa về Sài Gòn. Trên đường đi, An gặp Cường ở địa điểm C rồi gặp Bình ở địa điểm D. Tính vận tốc của mỗi người, biết rằng quãng đường Sài Gòn - Biên Hòa dài 39 km; CD = 6 km; Vận tốc của An bằng 1,5 vận tốc của Bình và bằng $\dfrac{3}4$ vận tốc của Cường.
Bài 4. (6 điểm)
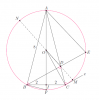
Cho tam giác $ABC$ cân tại $A$, nội tiếp đường tròn $(O)$. Từ $B$ kẻ đường thẳng vuông góc với $OC$, đường thẳng này cắt $AC$ tại $D$ và cắt $(O)$ tại $E$ ($E$ khác $B$). Cho biết $AB = 8$ cm và $BC = 4$ cm, tính độ dài các đoạn thẳng $DE$, $OA$ và $OD$.
Bài 5. (4 điểm)
Hộp phô mai có dạng hình trụ, đường kính đáy $12,2$ cm và chiều cao $2,4$ cm.
a) Biết rằng 8 miếng phô mai được xếp nằm sát bên trong hộp và độ dày của giấy gói từng miếng không đáng kể. Hỏi thể tích của một miếng phô mai đó là bao nhiêu?
b) Tính diện tích giấy gói được sử dụng cho một miếng phô mai.
(Ghi kết quả gần dùng chính xác đến 1 chữ số thập phân sau dấu phẩy).
Bình luận của mình: Nội dung của đề thì không khó lắm, nhưng đòi hỏi phải làm trong 90 phút thì có lẽ là khá căng đối với các bạn...
Cho $x, y$ là các số thực sao cho $\dfrac{2}x - \dfrac{1}y = \dfrac{1}{2x+y}$. Tính giá trị của biểu thức $\dfrac{x^2}{y^2} + \dfrac{y^2}{x^2}$.
Bài 2. (3 điểm)
Cho $a, b, c$ là ba số thực sao cho $a+b = c-2$ và $ab = 2c^2-3c+1$. Tìm giá trị lớn nhất của biểu thức $P = a^2+b^2$.
Bài 3. (3 điểm)
An khởi hành từ Sài Gòn đi Biên Hòa. Sau đó 5 phút, Bình và Cường khởi hành từ Biên Hòa về Sài Gòn. Trên đường đi, An gặp Cường ở địa điểm C rồi gặp Bình ở địa điểm D. Tính vận tốc của mỗi người, biết rằng quãng đường Sài Gòn - Biên Hòa dài 39 km; CD = 6 km; Vận tốc của An bằng 1,5 vận tốc của Bình và bằng $\dfrac{3}4$ vận tốc của Cường.
Bài 4. (6 điểm)
Cho tam giác $ABC$ cân tại $A$, nội tiếp đường tròn $(O)$. Từ $B$ kẻ đường thẳng vuông góc với $OC$, đường thẳng này cắt $AC$ tại $D$ và cắt $(O)$ tại $E$ ($E$ khác $B$). Cho biết $AB = 8$ cm và $BC = 4$ cm, tính độ dài các đoạn thẳng $DE$, $OA$ và $OD$.
Bài 5. (4 điểm)
Hộp phô mai có dạng hình trụ, đường kính đáy $12,2$ cm và chiều cao $2,4$ cm.
a) Biết rằng 8 miếng phô mai được xếp nằm sát bên trong hộp và độ dày của giấy gói từng miếng không đáng kể. Hỏi thể tích của một miếng phô mai đó là bao nhiêu?
b) Tính diện tích giấy gói được sử dụng cho một miếng phô mai.
(Ghi kết quả gần dùng chính xác đến 1 chữ số thập phân sau dấu phẩy).
Bình luận của mình: Nội dung của đề thì không khó lắm, nhưng đòi hỏi phải làm trong 90 phút thì có lẽ là khá căng đối với các bạn...