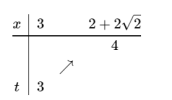[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
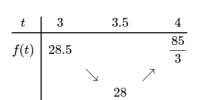
Cho bất phương trình [imath]m(\sqrt{x^2-4x+12}-1)+4x(4-x)-69\le 0[/imath] (m là tham số). Tìm tất cả các giá trị của m để bất phương trình trên nghiệm đúng với mọi [imath]x\in [3;2+2\sqrt2][/imath]
mn giúp mình bài này vs! Mình cảm ơn nhiều ạ ^^
mn giúp mình bài này vs! Mình cảm ơn nhiều ạ ^^
Attachments
Last edited by a moderator: