Cách giải khác bạn tham khảo nhé
[tex]w=\frac{2\pi }{T}=2\pi (rad/s)[/tex]
[tex]\Delta t = t2 - t1 = 0,25s[/tex]
Trong thời gian [tex]\Delta t[/tex], vecto bán kính quét được 1 cung: [tex]\Delta \varphi =w.\Delta t = 2\pi .0,25=\frac{\pi }{2}(rad)[/tex]
Giả sử ban đầu, điểm pha ở vị trí P1 trên hình. Từ P1 quay thêm 1 cung [tex]\frac{\pi }{2}[/tex] sẽ tới vị trí P2 như hình vẽ.
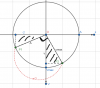
dễ thấy 2 trạng thái ở t1 và t2 là 2 trạng thái vuông pha
=> 2 tam giác gạch chéo trên hình đồng dạng
=> tỉ số: [tex]\frac{|-2|}{A}=\frac{|v|}{|v|max}=\frac{|v|}{|wA|}=>\frac{2}{1}=\frac{|v|}{w}=>|v|=|-2.w|=|-2.2\pi| =4\pi (cm/s) [/tex]
+, Nếu [tex]v = -4\pi (cm/s) < 0[/tex] => điểm P2 phải nằm ở nửa trên đường tròn
Vậy từ P2 ta quay ngược chiều dương 1 góc vuông sẽ xác định được P1.
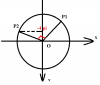
Mặt khác, tại P1, li độ của vật nhận giá trị âm, trong khi trường hợp này P1 không thể âm với bất kể vị trí nào của P2
=> [tex]v = -4\pi (cm/s)[/tex] Loại
+. Nếu [tex]v = 4\pi (cm/s) > 0[/tex] =>P2 nằm ở nửa dưới đường tròn => P1 hoàn toàn có thể nhận giá trị âm thỏa mãn
=> [tex]v = 4\pi (cm/s)[/tex] thỏa mãn
=> chọn A
-----
p/s: Cách giải này có thể hơi khó hiểu nhưng nếu nắm chắc được thì sẽ áp dụng rất hiệu quả trong các bài liên quan đến vuông pha nói riêng và dao động cơ nói chung ạ. Có thắc mắc gì tiếp tục trao đổi nè.
Bạn tham khảo thêm topic
Kĩ thuật dùng đường tròn để giải những bài dao động cơ và
Vòng tròn lượng giác đa trục trong dao động cơ để hiểu hơn nhé
Đừng quên ghé thăm
thiên đường Vật lí nữa nhe . Chúc bạn học tốt !
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Hocmai Forum 