- 8 Tháng năm 2017
- 1,000
- 2,492
- 349
- 27
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
"Võ công thiên hạ, mỗi người học 1 kiểu" - Trích Kim Dung.
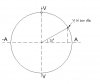
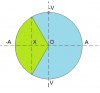
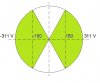
- Phương pháp đường tròn:
- Tư tưởng chính của phương pháp này là chuyển từ việc khảo sát phương trình dao động điều hòa với các yếu tố vận tốc, li độ, gia tốc, thời gian thay đổi phức tạp thành khảo sát chuyển động tròn đều đơn giản hơn.
- Ưu điểm của phương pháp này là trực quan, đơn giản, không gây nhầm lẫn, có thể giải quyết khoảng 80% - 85% các dạng bài dao động cơ. Tuy nhiên quan trọng nhất vẫn là sự vận dụng linh hoạt ở mỗi người - một thanh kiếm tốt trao vào tay người không biết dụng kiếm cũng vô ích.
- Phần giới thiệu đã xong, mình sẽ trình bày cách tiếp cận phương pháp và một số ứng dụng ở các bài viết sau.
- Phương pháp đường tròn:
Hồi học 12, khi biểu diễn dao động điều hòa lên đường tròn, mình đã nhận ra một mối tương quan đặc biệt giữa thời gian, li độ và vận tốc với các yếu tố hình học của đường tròn, từ đó xây dựng được một phương pháp rất mạnh để giải các bài giao động cơ - gọi là phương pháp đường tròn. Mấy năm gần đây phương pháp này không còn xa lạ đối với các bạn 12, nhưng ít ai biết một trong những người đầu tiên sử dụng và phát triển nó một cách đầy đủ nhất trên diễn đàn chính là mình.
- Tư tưởng chính của phương pháp này là chuyển từ việc khảo sát phương trình dao động điều hòa với các yếu tố vận tốc, li độ, gia tốc, thời gian thay đổi phức tạp thành khảo sát chuyển động tròn đều đơn giản hơn.
- Ưu điểm của phương pháp này là trực quan, đơn giản, không gây nhầm lẫn, có thể giải quyết khoảng 80% - 85% các dạng bài dao động cơ. Tuy nhiên quan trọng nhất vẫn là sự vận dụng linh hoạt ở mỗi người - một thanh kiếm tốt trao vào tay người không biết dụng kiếm cũng vô ích.
- Phần giới thiệu đã xong, mình sẽ trình bày cách tiếp cận phương pháp và một số ứng dụng ở các bài viết sau.
Last edited:
