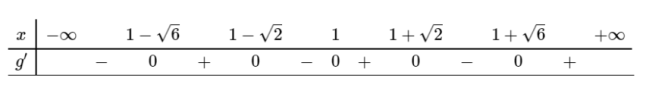Đặt [imath]t=5-2x\Rightarrow x=\dfrac{5-t}2[/imath]
[imath]f'(t)=a(x+2)(x-3)(x-5) (a>0)[/imath]
[imath]\Rightarrow f(t)=a\left(\dfrac{5-t}2+2\right).\left(\dfrac{5-t}2-3\right).\left(\dfrac{5-t}2-5\right)[/imath]
[imath]=\dfrac{-a}8(t-9)(t+1)(t+5)[/imath]
[imath]\Rightarrow f(t)=0\Leftrightarrow t=9; t=-1; t=-5[/imath]
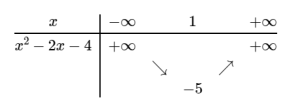
[imath]g(x)=f(x^2-2x-4); g'(x)=(2x-2)f'(x^2-2x-4)[/imath]
[imath]g'(x)=0\Leftrightarrow x=1[/imath] hoặc [imath]f'(x^2-2x-4)=0[/imath]
[imath]f'(x^2-2x-4)=0\left[\begin{matrix}x^2-2x-4=9 (1) \\x^2-2x-4=-1(2)\\x^2-2x-4=-5(3)\end{matrix}\right.[/imath]
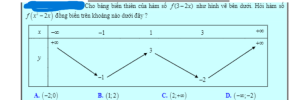
View attachment 214276
[imath]\Rightarrow (1);(2)[/imath] có 2 nghiệm p/b; [imath](3)[/imath] có nghiệm kép
Vậy [imath]g'(x)[/imath] có 5 điểm cực trị
Có gì khúc mắc em hỏi lại nha
Ngoài ra, em xem thêm tại
Hàm số và ứng dụng của đạo hàm
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.