Một lò xo treo thẳng đứng đầu dưới màn quả cầu có kl 200g, k = 1.25N/m, g = 10m/s.
A. Từ VTCB kéo vật xuống 1 đoạn rồi buông, biết trong khoảng tg t=3,2π (s) đi được quảng đường 48cm. Cho chiều dương hướng xuống, viết ptdđ.
B. Tính vận tốc khi động năng = 2 lần thế năng
C. Tính lực đàn hồi khi vật có vận tốc là 2,5cm/s
Sơ Tranh
[imath]a/[/imath]
Tần số góc: [imath]\omega = \dfrac{k}{m}=2,5 \ rad/s[/imath]
Trong thời gian [imath]t=3,2\pi[/imath] điểm pha đã quét được cung: [imath]\Delta \varphi = \omega . t = 2,5 .3,2\pi=8\pi = 4. 2\pi[/imath]
Quãng đường đi được: [imath]S= 4. 4A = 48cm \Rightarrow A= 6cm[/imath]
[imath]t=0[/imath] vật ở biên dương, vậy phương trình dao động: [imath]x=6\cos(2,5t)cm[/imath]
[imath]b/[/imath]
Câu này mình nghĩ tính tốc độ thì hợp lí hơn ấy :>
Gọi [imath]W,W_đ, W_t[/imath] lần lượt là cơ năng, động năng, thế năng vật
Theo đề ra: [imath]W_đ = 2W_t[/imath]
Mà: [imath]W_đ + W_t = W[/imath]
[imath]\Rightarrow W_t = \dfrac{1}{3}W \hArr \dfrac{1}{2}kx^2 = \dfrac{1}{3}.\dfrac{1}{2}kA^2[/imath]
[imath]\hArr x = \pm \dfrac{A}{\sqrt{3}}[/imath]
Ta xác định được [imath]4[/imath] vị trí điểm pha thỏa mãn như hình trên
Từ hình vẽ: [imath]A\cos \alpha = \dfrac{A}{\sqrt{3}}[/imath]
[imath]\alpha \approx 54,7^{\circ}[/imath]
Tốc độ vật tại đó:
Ta chiếu qua trục [imath]Ov[/imath]
[imath]v=v_{max}\sin \alpha=\omega A \sin \alpha \approx 12,24 cm/s[/imath] |  |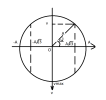
[imath]c/[/imath]
Tốc độ cực đại: [imath]v_{max}=\omega A = 15cm/s[/imath]
Độ dãn lò xo tại vị trí cân bằng: [imath]\Delta l_0 =\dfrac{mg}{k}=1,6m=160cm[/imath]
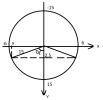
TH1: điểm pha của vật là điểm bên trái như hình
Ta có: [imath]15\cos \alpha = 2,5 \hArr \alpha \approx 80,4^{\circ}[/imath]
Tại đó vật có li độ: [imath]x=-A\sin \alpha \approx -5,92cm = -0,0592m[/imath]
Độ lớn lực đàn hồi: [imath]F_{dh}=k.(1,6-0,0592)=1,926N[/imath]
Th2: Điểm pha của vật là điểm bên phải:
tương tự ta cũng có [imath]\alpha \approx 80,4^{\circ}[/imath] và li độ [imath]x=0,0592m[/imath]
Độ lớn lực đàn hồi: [imath]F_{dh}=k.(1,6+0,0592)=2,074N[/imath]
|  |
Chúc bạn học tốt!
---------
Xem thêm:
Vòng tròn lượng giác đa trục trong dao động cơ |
Kĩ thuật dùng đường tròn để giải những bài dao động cơ
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Hocmai Forum 