Em xin lỗi vì 2 lần rồi đều gửi muộn ạ

Câu 1 :
a) $x^2=4x-4$
\Leftrightarrow $ x^2 - 4x + 4 = 0$
\Leftrightarrow $ (x-2)^2 = 0$
\Leftrightarrow $x-2=0$
\Leftrightarrow $x=2$
Vậy nghiệm của phương trình là x=2
b) $x^4=12x+5$
\Leftrightarrow $x^4 - 12x - 5=0$
\Leftrightarrow $(x^4 -2x^3-x^2) + (2x^3 -4x^2-2x) + (5x^2 - 10x -5) = 0$
\Leftrightarrow $(x^2 + 2x + 5)(x^2 -2x -1)=0$
Mặt khác : $x^2 + 2x + 5 = (x+1)^2 + 4 > 0$
Do đó : $x^2 - 2x - 1 = 0$
\Leftrightarrow $ x^2 -2x+1=2$
\Leftrightarrow $(x-1)^2 = 2$
\Leftrightarrow $\left[\begin{matrix}x-1=\sqrt{2} \\ x-1=-\sqrt{2} \end{matrix}\right.$
\Leftrightarrow $ \left[\begin{matrix}x=1 + \sqrt{2} \\ x= 1-\sqrt{2} \end{matrix}\right.$
Vậy nghiệm của phương trình là $ x=1 + \sqrt{2} ; x= 1-\sqrt{2}$
c) $15x^4 -8x^3 - 15x^2 + 4x + 4 = 0$
\Leftrightarrow $(15x^4 - 15x^3) + ( 7x^3 - 7x^2) - (8x^2 - 8x) - (4x-4) = 0$
\Leftrightarrow $(x-1)(15x^3 + 7x^2 - 8x -4)=0$
\Leftrightarrow $(x-1)(15x^3 + 10x^2 - 3x^2 -2x -6x-4)=0$
\Leftrightarrow $(x-1)(3x+2)(5x^2 - x -2)=0$
\Leftrightarrow $\left[\begin{matrix} x=1\\ x=1=\dfrac{-2}{3}\\ x= \dfrac{1+\sqrt{41}}{10} \\ x=\dfrac{1-\sqrt{41}}{10}\end{matrix}\right.$
Vậy tập nghiệm của phương trình là $S= \left\{ \dfrac{-2}{3};\dfrac{1-\sqrt{41}}{10};\dfrac{1+\sqrt{41}}{10};1 \right\} $
Bài 3 :

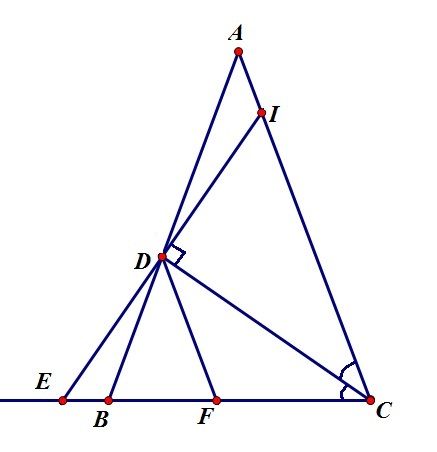
Xét tam giác ABM có : BE vuông góc với AM tại E
$ \to S_{ABM} = \dfrac{BE.AM}{2}$
Tương tự : $ \to S_{ACM} = \dfrac{CF.AM}{2}$
Ta có : $S_{ABC} = S_{ABM} + S_{ACM} = \dfrac{BE.AM}{2} + \dfrac{CF.AM}{2}$
$ \to \dfrac{2S_{ABC}}{AM} = BE + CF$
Vì $S_{ABC}$ không đổi nên BE + CF đạt giá trị nhỏ nhất khi AM lớn nhất.
Vẽ AD vuông góc BC tại D
TH1 : AC > AB
Ta có: HC và HB lần lượt là hình chiếu của đường xiên AC và AB kẻ từ A đến BC;
mà AC > AB
Do đó : DC > DB ( quan hệ đường xiên hình chiếu )
Lại có : DM là hình chiếu của đường xiên AM kẻ từ A đến BC.
\Rightarrow AM lớn nhất khi DM lớn nhất
Mà DM lớn nhất khi DM = DC ( vì M nằm trên BC) \Rightarrow M trùng với C
\Rightarrow M trùng với C thì BE + CF đạt giá trị nhỏ nhất.
Tương tự :
- TH2 : AB > AC thì BE + CF đạt giá trị nhỏ nhất khi M trùng với B.
- TH3 : AB = AC thì Be + CF đạt giá trị nhỏ nhất khi M trùng với B hoặc C.
Vậy BE + CF đạt giá trị nhỏ nhất khi M trùng với đỉnh tạo với A cạnh dài nhất trong tam giác ABC.
Bài 4 :
Đặt $A=20(m^2 + n^2 + p^2) + \dfrac{14(mn + np + mp)}{mn^2 + np^2 + pm^2}$
Ta có :
$ m+n+p=3 \\ \to 3(m^2 + n^2 + p^2) = (m+n+p)(m^2 + n^2 + p^2) = m^3 + mn^2 + mp^2 + n^3 + m^2n + np^2 + p^3 + m^2p + n^2p$
Lại có : $(\sqrt{m}^3 - \sqrt{m}p)^2 \ge 0$ \Leftrightarrow $m^3 + mp^2 \ge 2pm^2$
Tương tự ta có : $n^3 + nm^2 \ge 2mn^2; p^3 + pn^2 \ge 2np^2$
Suy ra : $3(a^2 + b^2 + c^2) \ge 3( mn^2 + np^2 + pm^2 ) \to a^2 + b^2 + c^2 \ge mn^2 + np^2 + pm^2 $
Do đó :
$A=20(m^2 + n^2 + p^2) + \dfrac{14(mn + np + mp)}{mn^2 + np^2 + pm^2} \ge 20(m^2 + n^2 + p^2) + \dfrac{14(mn + np + mp)}{m^2 + n^2 + p^2}$
\Leftrightarrow $A \ge 20(m^2 + n^2 + p^2) + \dfrac{7(m+n+p)^2 - 7(m^2+n^2+p^2)}{m^2 + n^2 + p^2}$
\Leftrightarrow $A \ge 20(m^2 + n^2 + p^2) + \dfrac{63}{m^2 + n^2 + p^2} - 7$
Ta có : $(m-n)^2 + (n-p)^2 + (p-m)^2 \ge 0$ \Leftrightarrow $m^2 + n^2 + c^2 \ge mn + np + mp$ \Leftrightarrow $9=(m+n+p)^2 \le 3(m^2 + n^2 + c^2)$ \Leftrightarrow $ 3 \le m^2 + n^2 + c^2p$
Đặt $m^2 + n^2 + p^2 = a \to a \ge 3$, ta có :
$A \ge 20a + \dfrac{63}{a} - 7 \ge 60 + 21 - 7 = 74$
Dấu "=" xảy ra khi m=n=p=1
Vậy GTNN của biểu thức đã cho là 74, đạt được khi m=n=p=1
* Câu hỏi phụ :
Con còn lại trên cầu lông của bò ( đề không hỏi là lông màu gì )