Câu 1: Ta có:
$\dfrac{ (x^2+a)(1+a)+a^2x^2+1}{(x^2-a)(1-a)+a^2x^2+1}= \dfrac{ x^2+ax^2+a+a^2+a^2x^2+1}{x^2-ax^2-a+a^2+a^2x^2+1} = \dfrac{ x^2(a^2+a+1)+(a^2+a+1)}{x^2(a^2-a+1)+(a^2-a+1)}=\dfrac{ (x^2+1)(a^2+a+1)}{(x^2+1)(a^2-a+1)}=\dfrac{ a^2+a+1}{a^2-a+1}$
Vậy giá trị của biểu thức ban đầu không phụ thuộc vào giá trị của x
Câu 2:
a) ĐKXĐ:
$\begin{cases}
4+8x \ne 0 \\
12x-6 \ne 0 \\
3(4-16x^2) \ne 0
\end{cases}
\leftrightarrow
\begin{cases}
x \ne \dfrac{ 1}{2} \\
x \ne -\dfrac{ 1}{2}
\end{cases} $
Với điều kiện trên phương trình đã cho tương đương:
$\dfrac{3(1+8x)(2x-1)}{3(2x-1).4(2x+1)}-\dfrac{ 8x(2x+1)}{2.6(2x-1)(2x+1)}+\dfrac{ 32x^2}{3.4(1+2x)(1-2x)} = 0\\
\leftrightarrow \dfrac{ 3(16x^2-6x-1)}{12(2x-1)(2x+1)}-\dfrac{ 16x^2+8x}{12(2x-1)(2x+1)}-\dfrac{ 32x^2}{12(2x-1)(2x+1)}= 0\\
\leftrightarrow \dfrac{ 48x^2-18x-3-16x^2-8x-32x^2}{12(2x-1)(2x+1)}=0 \\
\leftrightarrow \dfrac{ -26x-3}{12(2x-1)(2x+1)}=0 \\
\rightarrow -26x-3=0 $
$x=-\dfrac{ 3}{26}$ (thoả mãn điều kiện)
Vậy, phương trình đã cho có nghiệm duy nhất: $x=-\dfrac{ 3}{26}$
b) ĐKXĐ: $x \in R$
Với điều kiện trên phương trình đã cho tương đương:
$x^3+12=3x^2+4x \\
\leftrightarrow x^3-3x^2-4x+12=0 \\
\leftrightarrow x^3-2x^2-x^2+2x-6x+12=0 \\
\leftrightarrow x^2(x-2)-x(x-2)-6(x-2)=0 \\
\leftrightarrow (x-2)(x^2-x-6)=0 \\
\leftrightarrow (x-2)(x^2-3x+2x-6)=0 \\
\leftrightarrow (x-2)[x(x-3)+2(x-3)]=0 \\
\leftrightarrow (x-2)(x-3)(x+2)=0\\
\leftrightarrow
\left[ \begin{array}{ll}
x-2=0 \\
x-3=0 \\
x+2=0
\end{array} \right.
\leftrightarrow
\left[ \begin{array}{ll}
x=2 \\
x=3 \\
x=-2
\end{array} \right.$
Vậy, phương trình có 3 nghiệm: $x=2;x=3;x=-2$
Câu 3:
Vì $x+y+z=0 \\
\rightarrow y=-x-z \\
4xy=-4x^2-4xz \\
4xy-z^2=4x^2-4xz-z^2=-(2x+z)^2=-(x-y)^2$
Tương tự:
$4yz-x^2=-(y-z)^2 \\
4xz-y^2=-(z-x)^2$
Lại có:
$x=-y-z \\
x^2=-xy-xz \\
2x^2+yz=x^2+yz-xz-xy=(x-y)(x-z) $
Tương tự:
$2y^2+xz=(y-x)(y-z) \\
2z^2+xy=(z-x)(z-y)$
Như vậy:
$A.B.C=\dfrac{-(x-y)^2(y-z)^2(z-x)^2}{(x-y)(x-z)(y-x)(y-z)(z-x)(z-y)}=1$
Vậy nếu $x+y+z=0$ thì $ABC=1$
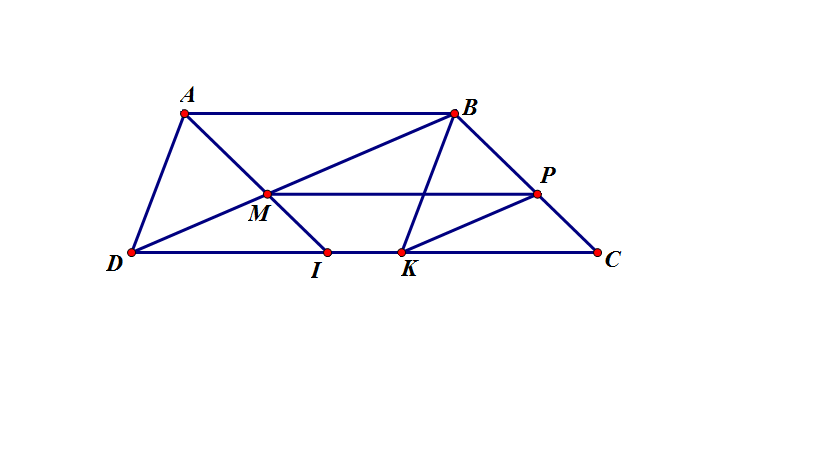
Câu 4:
Ta có:
Vì MI // BC (giả thiết) nên theo định lý Ta-lét:
$\dfrac{ DM}{DB} = \dfrac{ DI}{DC}$
(1)
Vì PK // BD (giả thiết) nên theo định lý Ta-lét:
$\dfrac{ CP}{CB}=\dfrac{ CK}{CD}$
(2)
Ta lại có:
Vì AD // BK và AB // DK nên ABKD là hình bình hành
Do đó AB=DK (*)
Tương tự: ABCI là hình bình hành
nên AB=IC (*)(*)
Từ (*) và (*)(*) ta có: DK=IC
<=> DK-IK=IC-IK
<=> DI=KC
(3)
Kết hợp
(1), (2), (3) ta có:
$\dfrac{ DM}{DB}=\dfrac{ DI}{DC}=\dfrac{CK}{DC}=\dfrac{ CP}{CB} \\
\dfrac{ DM}{DB}=\dfrac{ CP}{CB} \\
1-\dfrac{ DM}{DB}=1-\dfrac{ CP}{CB} \\
\dfrac{ MB}{BD}=\dfrac{ BP}{BC}$
Do đó MP//DC (định lý Ta-lét đảo)
Câu hỏi phụ
1) đó là chữ M và T, ghép là là MT (em-ti -- empty nghĩa là trống rỗng)
2) Vì Minh mang theo nghĩa là cầm theo đôi giày chứ bạn ấy không hề mặc đôi giày
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
| 19,25
