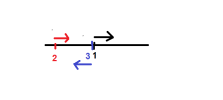
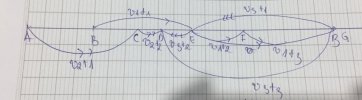
cùng một lúc hai người chuyển động đều, cùng chiều nhau với vận tốc v1=40km/h v2=30 km/h, cách nhau một quãng L. Cùng lúc đó người thứ ba ở vị trí người thứ nhất nhưng chuyển động ngược chiều hai người trên. Khi gặp người thứ hai người thứ ba lập tức quay lại đuổi theo người thứ nhất với vận tốc như cũ là v3=50 km/h. Kể từ khi gặp người thứ 2 đến khi đuổi kịp người thứ nhất người thứ ba đi hết 5,4 phút .
a)tính khoảng cách L
b)khi gặp người thứ nhất , họ cách người thứ hai bao xa
Mọi người vẽ sơ đồ giúp em với ạ
Lynn1512Bài em gửi kí hiệu gọi và trình bày còn chưa rõ ràng, chị hiểu ý tưởng bài của em rồi.
Dưới đây chị xin tiếp tục chữa bài theo bạn BQT bên trên nhé!
Ta có sơ đồ minh họa như sau:
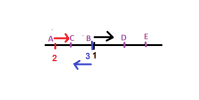
Với A,B lần lượt là điểm xuất phát ban đầu của người thứ 2 và người thứ nhất cùng với chiều chuyển động được miêu tả như hình, theo bài ra AB=L. C là vị trí người thứ 3 gặp người thứ 2, thời điểm đó người thứ nhất đã đi được 1 đoạn là BD. Cuối cùng là tại C, người thứ 3 quay lại đuổi theo người thứ nhất và gặp người thứ nhất tại E.
Từ những phân tích và sơ đồ trên em có thể suy ra những gì?
+) Tổng quãng đường người thứ 2 và người thứ 3 đi được kể từ lúc xuất phát đến lúc gặp nhau bằng L. Tức AC+ CB= L
+) Thời gian đi quãng đường AC của người thứ 2 bằng thời gian đi quãng đường BD của người thứ 3.
+) Với ý b, em hiểu là người thứ 3 gặp được người thứ nhất ở E, thì kể từ lúc gặp người thứ 3, người thứ hai đã đi được 1 đoạn CF nhưng em không thể biết chính xác F nằm ở khoảng CB hay BD hay DE nên chị không kí hiệu trong hình. Em hiểu là 1 điểm F trên đoạn CE. Khi đó, thời gian đi đoạn CF của người thứ 2 cũng bằng thời gian đi đoạn CE của người thứ ba.
*Đi vào giải chi tiết.
+) Gọi [imath]t_1[/imath] là thời gian đi đoạn BC của người thứ 3. Thì thời gian đi quãng đường AC của người 2 cũng là [imath]t_1[/imath]
+) Gọi [imath]t_2[/imath] là thời gian đi đoạn CE của người thứ 3. (bài cho [imath]t_2=5,4p=0,09(h)[/imath]
+) Gọi [imath]t[/imath] là thời gian đi quãng đường AE của người thứ nhất thì [imath]t=t_1+t_2[/imath]
a, Theo bài ra ta có hệ phương trình:
[imath]\left\{\begin{matrix} AC+CB=AB=L\\ CB+BE=CE \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} v_2t_1+v_3t_1=L\\ v_3t_1+v_1t=v_3t_2 \end{matrix}\right.[/imath]
Thay số và giải hệ trên em tìm được: [imath]t_1=0,01(h); L=0,8(km)[/imath]
b, Khoảng cách cần tìm là đoạn [imath]FE=CE-CF=v_3t_2-v_2t_2=1,8(km)[/imath]
Bài chị phân tích hơi dài, em đọc kĩ để hiểu nhé.
Chúc em học tốt!
Xem thêm:
Tạp chí Vật lí số 07 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.