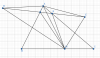
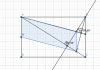
Cho hình thoi ABCD có Â=60 độ, điểm M nằm giữa 2 điểm A, D. Hai đường thẳng CM và AB cắt nhau tại N. Điểm K di động trên đoạn BD. Chứng minh độ dài đường chéo AC bằng tổng khoảng cách từ điểm K đến bốn cạnh của hình thoi ABCD
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
- Status
- Không mở trả lời sau này.
co 3 xe o to khoi hanh cung mot luc tu dia diem A den B .Do van toc xe thu nhat lon hpn xe thu 2 15km/h va lon hon xe thu 3 20km/h nen den B som hon xe thu 2 30 phut va xe thu 3 45 phut.Tinh van toc moi xe
1.Cho đường tròn tâm O có 2 dây cung AB và CD (CD<AB). các tia AB và CD cắt nhau tại E nằm ngoài đường tròn . Chứng minh EC<EA.
Bài 1) Cho tam giác ABC, một đường thẳng chia đôi diện tích tam giác cắt AB và BC tại M và N. Chứng minh rằng
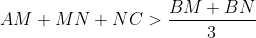
Bài 2) Cho tam giác ABC có đường cao AH, phân giác AD, trung tuyến AM
a) Chứng minh D nằm giữa H và M hoặc D trùng H trùng M.
b) Tìm điều kiện để D là trung điểm của HM.
c) Tính các góc của tam giác ABC nếu
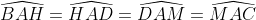
P/S: Mình là thành viên mới, mong các bạn giúp đỡ nha


Bài 2) Cho tam giác ABC có đường cao AH, phân giác AD, trung tuyến AM
a) Chứng minh D nằm giữa H và M hoặc D trùng H trùng M.
b) Tìm điều kiện để D là trung điểm của HM.
c) Tính các góc của tam giác ABC nếu
P/S: Mình là thành viên mới, mong các bạn giúp đỡ nha
Tam giác nhọn ABC có M thuộc BC; D đối xứng với M qua AB; E đối xứng với M qua AC; biết góc BAC=70.
DE cắt AB tại I, DE cắt AC tại K.
a) tâm giác ADE cân
b) MA là tia phân giác của góc IMK
c) tính các góc của tam giác ADE
***Giúp e với...
DE cắt AB tại I, DE cắt AC tại K.
a) tâm giác ADE cân
b) MA là tia phân giác của góc IMK
c) tính các góc của tam giác ADE
***Giúp e với...
cho hình chữ nhật ABCD kẻ BH vuông góc vs AC gọi K, M,N lần lượt là trung điểm của HC, AD,BH
a)c/m BK vuông góc vs AN
b) ANKM là hình bình hành từ đó suy ra BK vuông góc
a)c/m BK vuông góc vs AN
b) ANKM là hình bình hành từ đó suy ra BK vuông góc
Bài 13:
Cho tam giác ABC vuông tại C (CA<CB) từ C kẻ CH vuông góc với AB ( H thuộc AB, H khác B,A ) Kẻ HK và HQ lần lượt vuông góc BC, CA. Gọi M là trung điểm AB, qua B kẻ đường thẳng d vuông góc AB. a) CMR HKCQ là hình chữ nhật; b) CMR MC vuông góc KQ; c) Đường thẳng đi qua C vuông góc CM cắt đường thẳng d tại I, CMR IA đi qua trung điểm KQ (giúp mình với)
- 6 Tháng tám 2017
- 592
- 263
- 134
- 21
- Phú Yên
- THCS Huỳnh Thúc Kháng
a)Vì [tex]\widehat{CKH}=\widehat{QCK}=\widehat{HQC}=90[/tex]Bài 13:
Cho tam giác ABC vuông tại C (CA<CB) từ C kẻ CH vuông góc với AB ( H thuộc AB, H khác B,A ) Kẻ HK và HQ lần lượt vuông góc BC, CA. Gọi M là trung điểm AB, qua B kẻ đường thẳng d vuông góc AB. a) CMR HKCQ là hình chữ nhật; b) CMR MC vuông góc KQ; c) Đường thẳng đi qua C vuông góc CM cắt đường thẳng d tại I, CMR IA đi qua trung điểm KQ (giúp mình với)
nên HKCQ là hình chữ nhật
b)Gọi O là trung điểm của CH
Xét tam giác COK có CO=OK nên tam giác COK cân tại O
Suy ra [tex]\widehat{OCK}=\widehat{OKC}[/tex]
Vì CM là trung tuyến trong tam giác vuông ABC nên CM=MB=MA
Suy ra tam giác CMB cân tại M
Ta có [tex]\widehat{MCK}+\widehat{OKC}=\widehat{OCK}+\widehat{MBK}=90[/tex]
Suy ra MC vuông góc KQ


 Hê lu cả nhà!!!
Hê lu cả nhà!!! 

 Vậy là chúng mình đã kết thúc kì thi học kì 1, không biết các bạn học sinh của Diễn đàn làm bài có tốt không nhỉ? Và để mở đầu cho kì 2 thật rực rỡ, Diễn đàn sẽ gửi đến các bạn topic Chuyên đề hình học phẳng, đây là một topic rất "chất" hệ thống lại kiến thức hình học lớp 8. Cùng nhau xem lại và cmt thêm thật nhiều kiến thức và bài tập hình học ở dưới topic này nhé
Vậy là chúng mình đã kết thúc kì thi học kì 1, không biết các bạn học sinh của Diễn đàn làm bài có tốt không nhỉ? Và để mở đầu cho kì 2 thật rực rỡ, Diễn đàn sẽ gửi đến các bạn topic Chuyên đề hình học phẳng, đây là một topic rất "chất" hệ thống lại kiến thức hình học lớp 8. Cùng nhau xem lại và cmt thêm thật nhiều kiến thức và bài tập hình học ở dưới topic này nhé

 Chúc các bạn và gia đình một mùa Giáng sinh an lành và ấm áp
Chúc các bạn và gia đình một mùa Giáng sinh an lành và ấm áp


- Status
- Không mở trả lời sau này.