T
thinhrost1
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Trước hết là cách đăng hình lên diễn đàn
Phần mềm để vẽ hình:
- GSP viet ( tiếng Việt ) : nên có cái này cho tiện.Click here
- Bạn nào không biết cách sử dụng thì liên hệ với mình.
Cài đặt GSP
(Nếu không cài mật mã thì vẫn có thể dùng thử được)
Hoặc tải geogrebra tại đây (Click vào)
Sau khi vẽ xong các bạn có thể chụp lại màn hình và sửa chữa bằng cách sau:
Sau khi đến đây bạn nào làm không được có thể gửi tin nhắn cho mình qua đây
Có nhiều trang web hỗ trợ việc up ảnh lên diễn đàn, nhưng mình thấy sử photobucket là ổn định và an toàn nhất. Biết sử dụng hợp lý ảnh sẽ không xóa mất như các trang web.
Tuy vậy đòi hỏi một chút là đăng ký tài khoản, từ đó dễ dàng up các ảnh thi đấu, offline, chém gió, hình học,.. lên diễn đàn.
- Bước 1: Vào trang http://photobucket.com
- Bước 2: Bấm nút sign up, cửa sổ Sign up for Photobucket. It's Free! hiện ra như hình ở dưới. Cách đăng ký giống như ở diễn đàn, nên để tên và password trùng với nick HM để khỏi quên!
Bước 3: Đăng nhập vào photobucket, nên lưu lại để lần sau đỡ phải khai báo lằng nhằng...
- Bước 4: Bấm nút Upload màu cam
- Bước 5: Cửa sổ Choose photos and videos hiện ra, bấm nút này và chọn 1 tập tin ảnh cần up.
- Bước 6: Cửa sổ sẽ hiện quá trình tải ảnh và khi thực hiện xong sẽ hiện cái hình nhỏ ở dưới góc bên trái bấm vào nó nó sẽ hiện hình to hơn sau đó các bạn đưa con trỏ chuột vào giữa hình và nháy chuột phải chọn "Sao chép URL hình ảnh" (hay cái gì đoại loại giống thế như Copy Url picture,...)
- Bước 7: Sau khi copy xong chọn Tab mà bạn đang đăng bài bấm vào Bỏ hình vào bài.
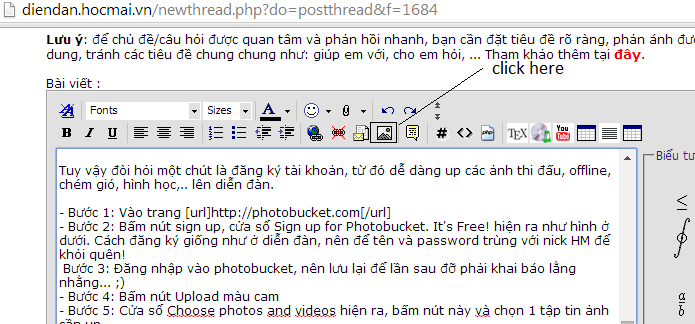
khi hộp thoại hiện ra dán link bạn vừa copy vào -> Nhấn Ok nó sẽ ra giống như vầy
Như thế là xong phần đăng ảnh lên rồi đó, bạn nào còn thắc mắc bước nào thì liên hệ với mình qua đây
Bây giờ vào vấn đề chính Topic này lập ra giúp các bạn học sinh có thể trao đổi rõ hơn về các bài toán hay và khó. Và không những thế, mình mong rằng chính những bài toán trong Topic này khi đã được mình và chính các bạn cẩn thận chọn lọc và sắp sếp một cách hợp lý sẽ giúp ích nhiều cho mình và các bạn trong việc ôn tập lại các nội dung kiến thức đã học, giúp các bạn tự tin hơn và cảm thấy thích thú hơn trong hoạt động giải toán hình học.
Xin lưu ý các bạn 1 quy định nhỏ để giúp Topic luôn được duy trì và phát triển: Một BT hình thuộc kiến thức lớp 7 hoặc lớp 8( khuyến khích lớp 8 vì đây là box toán 8) khi đã ở trên Topic này thì nó nên có lời giải sau khoảng 1 ngày, còn nếu nó chưa được giải bởi một ai đó thì người đưa ra BT cần đưa ra lời giải sau 1 ngày. Mình rất mong được các bạn ủng hộ và góp sức để Topic ngày một phát triển.
$\color{Blue}{\fbox{Các kiến thức cơ bản}}:$
$\bigstar \text{Chương I: Đa giác}$
$\fbox{I. Tam giác}$:
1. Hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tường ứng bằng nhau, các góc tương ứng bằng nhau.
Các trường hợp bằng nhau của tam giác
a) Trường hợp 1 : cạnh – cạnh – cạnhNếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằngnhau.
b) Trường hợp 2 : cạnh – góc – cạnhNếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tamgiác kia thì hai tam giác đó bằng nhau.
c) Trường hợp 3 : góc – cạnh – gócNếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tamgiác kia thì hai tam giác đó bằng nhau.
a') Trường hợp 1 : hai cạnh góc vuông (cạnh – góc - cạnh)Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giácvuông kia thì hai tam giác vuông đó bằng nhau.
b') Trường hợp 2 : cạnh huyền – góc nhọn (góc – cạnh – góc)Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một gócnhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
c') Trường hợp 3 : cạnh huyền – cạnh góc vuông (cạnh – cạnh – cạnh)Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền vàmột cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
2. Trong tam giác ABC:
-Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
-Ba đường cao đồng quy tại một điểm H gọi là trực tâm của tam giác
-Ba đường trung trực đồng quy tại điểm O gọi là tâm đường tròn ngoại tiếp tam giác
-Ba đường phân giác trong đồng quy tại một điểm I gọi là tâm đường tròn nội tiếp tam giác
-Ba đường trung tuyến đồng quy tại một điểm G gọi là trọng tâm của tam giác và AG=2GM (với M là trung điểm của BC)
$\fbox{II. Hình thang}$
- Tứ giác ABCD à hình thang

- Đoạn thẳng nối trung điểm hai cạnh bên gọi là đường trung bình hình thang.
-Đường trung bình hình thang song song với hai cạnh đáy và độ dài bằng nửa tổng độ dài hai đáy.
-Hình thang cân là hình thang có hai góc ở đáy bằng nhau
-Hình thang có hai đường chéo bằng nhau là hình thang cân và ngược lại
$\fbox{III. Hình bình hành}$
-Tứ giác có các cạnh đối song song là hình bình hành
-Tứ giác có các cạnh đối bằng nhau là hình bình hành.
-Tứ giác có hai cạnh đối vừa song song và vừa bằng nhau là hình bình hành.
-Tứ giác có các góc đối bằng nhau là hình bình hành.
-Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Để chứng minh 1 tứ giác là hình bình hành ta chứng minh tứ giác có một trong các tính chất sau:
a) Các cạnh đối bằng nhau.
b) Các góc đối bằng nhau.
c) Hai đường chéo cắt nhau tại trung điểm mỗi đường.
d) Một cặp cạnh đối song song và bằng nhau
e) Hai cặp cạnh song song
$\fbox{IV. Hình chữ nhật}$
-Hình chữ nhật là một tứ giác lồi có bốn góc vuông
-Hình chữ nhật là hình bình hành có một góc vuông.
-Hình bình hành trở thành hình chữ nhật khi hai đường chéo bằng nhau
Dấu hiệu nhận biết
-Tứ giác có ba góc vuông là hình chữ nhật.
-Hình thang cân có một góc vuông là hình chữ nhật.
-Hình bình hành có một góc vuông là hình chữ nhật.
-Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
$\fbox{V. Hình thoi và hình vuông}$
1) Hình thoi:
Hình thoi là một tứ giác có bốn cạnh bằng nhau.
*Dấu hiệu nhận biết tứ giác có phải là hình thoi hay không:
-Tứ giác có 4 cạnh bằng nhau là hình thoi
-Hình bình hành có:+ Có 2 cạnh kề bằng nhau là hình thoi
+Có 2 đường chéo vuông góc là hình thoi
+Có 1 đường chéo là đường phân giác của một góc là hình thoi
2)Hình vuông
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau
*Dấu hiệu nhận biết:
+Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+Hình chữ nhật có hai đường chéo vuông góc nhau là hình vuông.
+Hình chữ nhật có có một đường chéo là đường phân giác một góc là hình vuông.
+Hình thoi có một góc vuông là hình vuông.
+Hình thoi có hai đường chéo bằng nhau là hình vuông.
$\fbox{VI. Đa giác}$
-Đa giác đều là đa giác có tất cả các cạnh bằng nhau và các góc ở đỉnh bằng nhau
-Tổng số đo các góc của hình n-giác bằng $(n-2).180^o$
-Số đường chéo của hình n-giác là: $\dfrac{n(n-3)}{2}$. Suy ra: mỗi góc của đa giác đều n cạnh có số đo là $\dfrac{(n-2).180^o}{n}$
$\bigstar \text{Chương II: Tam giác đồng dạng}$
$\fbox{I. Định lí Ta-Lét trong tam giác}$
Định lí Ta-lét trong tam giác:
Cho tam giác ABC. B'C' lần lượt trên AB, AC.
Nếu $B'C'//BC$ thì: $\dfrac{AB'}{AB}=\dfrac{AC'}{AC}=\dfrac{BC'}{BC}$
Đảo lại nếu: $\dfrac{AB'}{AB}=\dfrac{AC'}{AC}$ thì $B'C'//BC$
Tính chất đường phân giác của tam giác:
AD,AE lần lượt là đường phân giác trong và phân giác ngoài của tam giác ABC. Ta có $AD \perp AE$ và $ \dfrac{DB}{DC}=\dfrac{EB}{EC}=\dfrac{AB}{AC}$
$\fbox{II. Tam giác đồng dạng}$
-Định nghĩa:
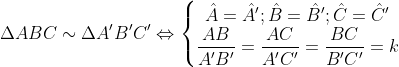
k được gọi là tỉ số đồng dạng.
-Các trường hợp đồng dạng:
a) Nếu $\hat A=\hat A' , \hat B=\hat B'$ thì tam giác ABC đồng dạng tam giác A'B'C'
b) Nếu
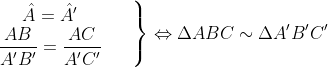
c) Nếu:
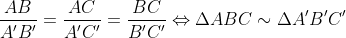
-Trường hợp đồng dạng của tam giác vuông:
Cho hai tam giác vuông ABC và A'B'C' với $\hat A=\hat A'=90^o.\Delta ABC \sim \Delta A'B'C'$ nếu một trong các trường hợp sau đây được thỏa mãn:
a) $\hat B=\hat B'$ hoặc $\hat C=\hat C'$
b) $\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}$
-Tỉ số hai đường phân giác, hai đường cao, hai đường trung tuyến, hai bán kính ngoại tiếp, hai bán kính nội tiếp, hai chu vi tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng
-Tỉ số hai diện tích đồng dạng thì bằng bình phương tỉ số đồng dạng
Xong phần kiến thức cơ bản, sau đó sẽ là các chuyên đề do bạn nhuquynhdat đưa lên
Phần mềm để vẽ hình:
- GSP viet ( tiếng Việt ) : nên có cái này cho tiện.Click here
- Bạn nào không biết cách sử dụng thì liên hệ với mình.
Cài đặt GSP
PHP:
mã là thongnong VUAUJR
mật khẩu D7F674FAHoặc tải geogrebra tại đây (Click vào)
Sau khi vẽ xong các bạn có thể chụp lại màn hình và sửa chữa bằng cách sau:
1. Đối với máy để bàn
Đầu tiên bạn cho màn hình hiển thị cảnh mà bạn muốn chụp:
Sau đó bạn nhấn vào phím PrintScreen bên phải phím F12
Sau đó các bạn nhấp trái chuột vào chữ “Start” nằm ở góc trái bên dưới, các bạn chọn “Run” và gõ mspaint.Sau khi chọn thành công, hệ thống sẽ chuyển bạn đến giao diện của chương trình Paint. Tại đây bạn đè Ctrl và nhấn chữ V. Hoặc có thể mở trực tiếp từ Start/ All program/ accessories/Paint.
Sau đó bạn có thể sử dụng các công cụ của chương trình Paint thêm vào các chú thích cần thiết.
0: Bạn có thể chọn một phần Bằng cách sử dụng công cụ sau:
Sau khi chọn phần đó bạn có thể sao chép( Copy hoặc Ctrl+C), Xóa (Delete) , Cắt (Cut hoặc Ctrl+X),..
P/s: Mình thường Copy khu vực quan rồi sau đó chọn tất cả (Crtl+A) -> Xóa-> Dán rồi sau đó đến bước 1 để thu nhỏ khu vực hoặc có thể thu nhỏ khu vực như bước 1 trước rồi dán sau cũng được
1: Bạn có thể đóng khung khu vực cần chú thích bằng cách đưa con trỏ chuột vào ô vuông nhỏ và sau đó kéo thả tại khu vực phù hợp.
2: Bạn có thể thêm chữ hoặc các dòng chú thích vào khu vực cần chú thích bằng cách bấm chữ A rồi sau đó chọn khu vực để thêm chữ cần chú thích.
2. Đối với laptop:
Nhấn đồng thời 2 phím Fn + printscreen hoặc alt + printscreen để chụp màn hình / rồi vào start / programs / accessories / mở paint lên / nhấn đồng thời 2 phím Ctrl + V để dán hình vào./ tiếp tục, bạn click vào File ( trong cửa sổ paint ) rồi chọn SAVE AS chọn kiểu file ảnh là .png rồi nhấp SAVE.
Nếu bạn nào muốn sử dụng paint hiệu quả hơn thì có thể xem tại đây
Sau khi đến đây bạn nào làm không được có thể gửi tin nhắn cho mình qua đây
Có nhiều trang web hỗ trợ việc up ảnh lên diễn đàn, nhưng mình thấy sử photobucket là ổn định và an toàn nhất. Biết sử dụng hợp lý ảnh sẽ không xóa mất như các trang web.
Tuy vậy đòi hỏi một chút là đăng ký tài khoản, từ đó dễ dàng up các ảnh thi đấu, offline, chém gió, hình học,.. lên diễn đàn.
- Bước 1: Vào trang http://photobucket.com
- Bước 2: Bấm nút sign up, cửa sổ Sign up for Photobucket. It's Free! hiện ra như hình ở dưới. Cách đăng ký giống như ở diễn đàn, nên để tên và password trùng với nick HM để khỏi quên!
Bước 3: Đăng nhập vào photobucket, nên lưu lại để lần sau đỡ phải khai báo lằng nhằng...
- Bước 4: Bấm nút Upload màu cam
- Bước 5: Cửa sổ Choose photos and videos hiện ra, bấm nút này và chọn 1 tập tin ảnh cần up.
- Bước 6: Cửa sổ sẽ hiện quá trình tải ảnh và khi thực hiện xong sẽ hiện cái hình nhỏ ở dưới góc bên trái bấm vào nó nó sẽ hiện hình to hơn sau đó các bạn đưa con trỏ chuột vào giữa hình và nháy chuột phải chọn "Sao chép URL hình ảnh" (hay cái gì đoại loại giống thế như Copy Url picture,...)
- Bước 7: Sau khi copy xong chọn Tab mà bạn đang đăng bài bấm vào Bỏ hình vào bài.

khi hộp thoại hiện ra dán link bạn vừa copy vào -> Nhấn Ok nó sẽ ra giống như vầy
PHP:
[IMG]http://i1275.photobucket.com/albums/y442/thinhrost1/Untitled_zps8503b33b.png[/IMG]Như thế là xong phần đăng ảnh lên rồi đó, bạn nào còn thắc mắc bước nào thì liên hệ với mình qua đây
Bây giờ vào vấn đề chính Topic này lập ra giúp các bạn học sinh có thể trao đổi rõ hơn về các bài toán hay và khó. Và không những thế, mình mong rằng chính những bài toán trong Topic này khi đã được mình và chính các bạn cẩn thận chọn lọc và sắp sếp một cách hợp lý sẽ giúp ích nhiều cho mình và các bạn trong việc ôn tập lại các nội dung kiến thức đã học, giúp các bạn tự tin hơn và cảm thấy thích thú hơn trong hoạt động giải toán hình học.
Xin lưu ý các bạn 1 quy định nhỏ để giúp Topic luôn được duy trì và phát triển: Một BT hình thuộc kiến thức lớp 7 hoặc lớp 8( khuyến khích lớp 8 vì đây là box toán 8) khi đã ở trên Topic này thì nó nên có lời giải sau khoảng 1 ngày, còn nếu nó chưa được giải bởi một ai đó thì người đưa ra BT cần đưa ra lời giải sau 1 ngày. Mình rất mong được các bạn ủng hộ và góp sức để Topic ngày một phát triển.
$\color{Blue}{\fbox{Các kiến thức cơ bản}}:$
$\bigstar \text{Chương I: Đa giác}$
$\fbox{I. Tam giác}$:
1. Hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tường ứng bằng nhau, các góc tương ứng bằng nhau.
Các trường hợp bằng nhau của tam giác
a) Trường hợp 1 : cạnh – cạnh – cạnhNếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằngnhau.
b) Trường hợp 2 : cạnh – góc – cạnhNếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tamgiác kia thì hai tam giác đó bằng nhau.
c) Trường hợp 3 : góc – cạnh – gócNếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tamgiác kia thì hai tam giác đó bằng nhau.
a') Trường hợp 1 : hai cạnh góc vuông (cạnh – góc - cạnh)Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giácvuông kia thì hai tam giác vuông đó bằng nhau.
b') Trường hợp 2 : cạnh huyền – góc nhọn (góc – cạnh – góc)Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một gócnhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
c') Trường hợp 3 : cạnh huyền – cạnh góc vuông (cạnh – cạnh – cạnh)Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền vàmột cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
2. Trong tam giác ABC:
-Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
-Ba đường cao đồng quy tại một điểm H gọi là trực tâm của tam giác
-Ba đường trung trực đồng quy tại điểm O gọi là tâm đường tròn ngoại tiếp tam giác
-Ba đường phân giác trong đồng quy tại một điểm I gọi là tâm đường tròn nội tiếp tam giác
-Ba đường trung tuyến đồng quy tại một điểm G gọi là trọng tâm của tam giác và AG=2GM (với M là trung điểm của BC)
$\fbox{II. Hình thang}$
- Tứ giác ABCD à hình thang
- Đoạn thẳng nối trung điểm hai cạnh bên gọi là đường trung bình hình thang.
-Đường trung bình hình thang song song với hai cạnh đáy và độ dài bằng nửa tổng độ dài hai đáy.
-Hình thang cân là hình thang có hai góc ở đáy bằng nhau
-Hình thang có hai đường chéo bằng nhau là hình thang cân và ngược lại
$\fbox{III. Hình bình hành}$
-Tứ giác có các cạnh đối song song là hình bình hành
-Tứ giác có các cạnh đối bằng nhau là hình bình hành.
-Tứ giác có hai cạnh đối vừa song song và vừa bằng nhau là hình bình hành.
-Tứ giác có các góc đối bằng nhau là hình bình hành.
-Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Để chứng minh 1 tứ giác là hình bình hành ta chứng minh tứ giác có một trong các tính chất sau:
a) Các cạnh đối bằng nhau.
b) Các góc đối bằng nhau.
c) Hai đường chéo cắt nhau tại trung điểm mỗi đường.
d) Một cặp cạnh đối song song và bằng nhau
e) Hai cặp cạnh song song
$\fbox{IV. Hình chữ nhật}$
-Hình chữ nhật là một tứ giác lồi có bốn góc vuông
-Hình chữ nhật là hình bình hành có một góc vuông.
-Hình bình hành trở thành hình chữ nhật khi hai đường chéo bằng nhau
Dấu hiệu nhận biết
-Tứ giác có ba góc vuông là hình chữ nhật.
-Hình thang cân có một góc vuông là hình chữ nhật.
-Hình bình hành có một góc vuông là hình chữ nhật.
-Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
$\fbox{V. Hình thoi và hình vuông}$
1) Hình thoi:
Hình thoi là một tứ giác có bốn cạnh bằng nhau.
*Dấu hiệu nhận biết tứ giác có phải là hình thoi hay không:
-Tứ giác có 4 cạnh bằng nhau là hình thoi
-Hình bình hành có:+ Có 2 cạnh kề bằng nhau là hình thoi
+Có 2 đường chéo vuông góc là hình thoi
+Có 1 đường chéo là đường phân giác của một góc là hình thoi
2)Hình vuông
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau
*Dấu hiệu nhận biết:
+Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+Hình chữ nhật có hai đường chéo vuông góc nhau là hình vuông.
+Hình chữ nhật có có một đường chéo là đường phân giác một góc là hình vuông.
+Hình thoi có một góc vuông là hình vuông.
+Hình thoi có hai đường chéo bằng nhau là hình vuông.
$\fbox{VI. Đa giác}$
-Đa giác đều là đa giác có tất cả các cạnh bằng nhau và các góc ở đỉnh bằng nhau
-Tổng số đo các góc của hình n-giác bằng $(n-2).180^o$
-Số đường chéo của hình n-giác là: $\dfrac{n(n-3)}{2}$. Suy ra: mỗi góc của đa giác đều n cạnh có số đo là $\dfrac{(n-2).180^o}{n}$
$\bigstar \text{Chương II: Tam giác đồng dạng}$
$\fbox{I. Định lí Ta-Lét trong tam giác}$
Định lí Ta-lét trong tam giác:
Cho tam giác ABC. B'C' lần lượt trên AB, AC.
Nếu $B'C'//BC$ thì: $\dfrac{AB'}{AB}=\dfrac{AC'}{AC}=\dfrac{BC'}{BC}$
Đảo lại nếu: $\dfrac{AB'}{AB}=\dfrac{AC'}{AC}$ thì $B'C'//BC$
Tính chất đường phân giác của tam giác:
AD,AE lần lượt là đường phân giác trong và phân giác ngoài của tam giác ABC. Ta có $AD \perp AE$ và $ \dfrac{DB}{DC}=\dfrac{EB}{EC}=\dfrac{AB}{AC}$
$\fbox{II. Tam giác đồng dạng}$
-Định nghĩa:
k được gọi là tỉ số đồng dạng.
-Các trường hợp đồng dạng:
a) Nếu $\hat A=\hat A' , \hat B=\hat B'$ thì tam giác ABC đồng dạng tam giác A'B'C'
b) Nếu
c) Nếu:
-Trường hợp đồng dạng của tam giác vuông:
Cho hai tam giác vuông ABC và A'B'C' với $\hat A=\hat A'=90^o.\Delta ABC \sim \Delta A'B'C'$ nếu một trong các trường hợp sau đây được thỏa mãn:
a) $\hat B=\hat B'$ hoặc $\hat C=\hat C'$
b) $\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}$
-Tỉ số hai đường phân giác, hai đường cao, hai đường trung tuyến, hai bán kính ngoại tiếp, hai bán kính nội tiếp, hai chu vi tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng
-Tỉ số hai diện tích đồng dạng thì bằng bình phương tỉ số đồng dạng
Xong phần kiến thức cơ bản, sau đó sẽ là các chuyên đề do bạn nhuquynhdat đưa lên
Last edited by a moderator: