N
niemkieuloveahbu
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Lên lớp 11 chúng ta dần làm quen với hình học không gian,vì lẽ đã quá quen với hình học trong mặt phẳng nên có nhiều bạn gặp khó khăn,vậy mình lập topic này cùng thảo luận và làm bài về hình không gian.
Trước hết, ta có chút quy định cho pic.
Nhằm giúp pic có một tiêu chí thống nhất, có một số điều chúng ta cần chú ý:
Để tiện cho việc theo dõi, quản lí cũng như tổng hợp sau này, mình xin thống nhất cách post bài cho các bạn ở các topic chú ý.
- Nếu post bài giải thì bạn viết như bình thường, chỉ dùng màu đen
- Hạn chế dùng các emoticon
- Các bài hướng dẫn cách giải các bạn post thành 1 bài riêng và dùng kiểu chữ đậm.
VD:
Bài 1
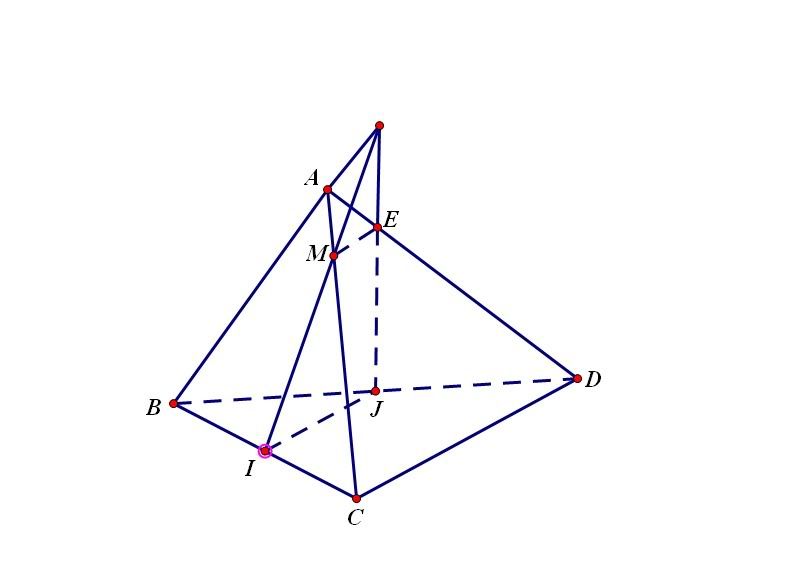
Cho hình chóp ABCD, gọi P,Q lần lượt là trung điểm của AB,CD, R là điểm thuộc BC sao cho BR=2RC, S là giao điểm của (QPR) với AD. Chứng minh rằng AS=2SD.
- Các bài viết phải theo đúng quy định của diễn đàn học mãi, viết hoa đầu dòng, tuyệt đối không được spam.
- Bài viết không sử dụng latex để viết các kí hiệu toán học sẽ bị xoá không giải thích
- Các thành viên để tiện liên lạc nên vào Chức năng -> Sửa thông tin chi tiết hoặc vào link này -> Tên Yahoo (yim) và gõ nick của mình.
Để vẽ hình học không gian, các bạn nên dùng chương trình GSP5 Việt hóa này Việt hóa
- Hướng dẫn
- Thêm chút nữa là nội quy post bài,các bạn xem kĩ tại Quy định(tớ lười nên sang đấy coi nhờ , ))
))
- Các bài giải post gộp vào một bài viết,tránh tình trạng spam,câu bài gây loãng pic.
- Vì đã nhắc nhở nên bạn nào cố tình vi phạm sẽ có hình thức phạt nhé.
-Còn vấn đề gì sẽ bổ sung sau.
 .
.
Thân
Hạ Kiều
Thanks Nhân giúp tớ soạn một bản hướng dẫn chi tiết nhé,
Chúc pic của chúng ta hoạt động sôi nổi,nhiệt tình! . Canh đúng giờ hoàng đạo,
. Canh đúng giờ hoàng đạo, )
)
:M02::M02::M02::M02::M02:
Trước hết, ta có chút quy định cho pic.
Nhằm giúp pic có một tiêu chí thống nhất, có một số điều chúng ta cần chú ý:
Để tiện cho việc theo dõi, quản lí cũng như tổng hợp sau này, mình xin thống nhất cách post bài cho các bạn ở các topic chú ý.
- Nếu post bài giải thì bạn viết như bình thường, chỉ dùng màu đen
- Hạn chế dùng các emoticon
- Các bài hướng dẫn cách giải các bạn post thành 1 bài riêng và dùng kiểu chữ đậm.
VD:
Bài 1
Cho hình chóp ABCD, gọi P,Q lần lượt là trung điểm của AB,CD, R là điểm thuộc BC sao cho BR=2RC, S là giao điểm của (QPR) với AD. Chứng minh rằng AS=2SD.
- Các bài viết phải theo đúng quy định của diễn đàn học mãi, viết hoa đầu dòng, tuyệt đối không được spam.
- Bài viết không sử dụng latex để viết các kí hiệu toán học sẽ bị xoá không giải thích
- Các thành viên để tiện liên lạc nên vào Chức năng -> Sửa thông tin chi tiết hoặc vào link này -> Tên Yahoo (yim) và gõ nick của mình.
Để vẽ hình học không gian, các bạn nên dùng chương trình GSP5 Việt hóa này Việt hóa
- Hướng dẫn
- Thêm chút nữa là nội quy post bài,các bạn xem kĩ tại Quy định(tớ lười nên sang đấy coi nhờ ,
- Các bài giải post gộp vào một bài viết,tránh tình trạng spam,câu bài gây loãng pic.
- Vì đã nhắc nhở nên bạn nào cố tình vi phạm sẽ có hình thức phạt nhé.
-Còn vấn đề gì sẽ bổ sung sau.
Thân
Hạ Kiều
Thanks Nhân giúp tớ soạn một bản hướng dẫn chi tiết nhé,
Chúc pic của chúng ta hoạt động sôi nổi,nhiệt tình!
:M02::M02::M02::M02::M02: