- 28 Tháng một 2016
- 3,897
- 1
- 8,081
- 939
- Yên Bái
- THPT Lê Quý Đôn <3
Hà Nội một ngày mưa...
Nếu bạn là một người học không tốt môn vật lí? Không biết bắt đầu từ đâu? Không biết phân dạng cũng như cần tìm hướng dẫn chi tiết từng phần của môn học này thì đây là topic dành cho bạn! Mình không đảm bảo nó hữu ích với tất cả mọi người nhưng mình sẽ cố gắng trình bày một cách dễ hiểu, xúc tích và cô đọng nhất!
Chuỗi [Chuyên đề] Tổng hợp kiến thức vật lí sẽ diễn ra ở các khối 9,10,11 và 12. Các bạn chú ý theo dõi để đón nhận nhé!
PHẦN A: Kiến thức cơ bản lực điện, điện tích trong điện trường
PHẦN B: Một số dạng toán về lực điện, điện tích trong điện trường
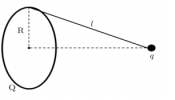
I, Lực tương tác giữa hai điện tích (Lực Cu-lông)
- Khi hai điện tích điểm đứng yên đặt gần nhau trong môi trường điện môi đồng chất thì giữa chúng có lực tương tác điện (hay lực tương tác Cu-lông)
- Vecto lực tương tác giữa 2 điện tích đứng yên trong môi trường điện môi đồng tính có đặc điểm:
- Xung quanh điện tích có điện trường, điện trường là một dạng vật chất bao quanh các điện tích và gắn liền với điện tích. Điện trường tác dụng lực điện lên điện tích khác đặt trong nó.
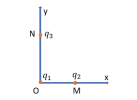
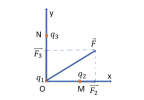
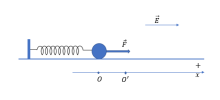
- Đại lượng đặc trưng cho độ mạnh yếu của điện trường về phương diện lực tác dụng lực và cường độ điện trường [imath]\vec{E}[/imath] có đặc điểm:
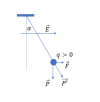
- Lực điện [imath]\vec{F}[/imath] cùng chiều với điện trường [imath]\vec{E}[/imath] khi [imath]q[/imath] là điện tích dương, ngược chiều [imath]\vec{E}[/imath] khi [imath]q[/imath] là điện tích âm.
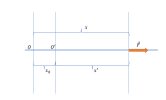
|||, Công của lực điện trường
- Khi một điện tích [imath]q[/imath] đặt trong điện trường, thì nó sẽ bị lực điện trường di chuyển và sinh công.
- Nếu điện trường đều thì công di chuyển của điện tích là [imath]A=qEd[/imath] với [imath]d[/imath] là hình chiếu của độ dời lên phương đường sức.
- Đại lượng đặc chưng cho khả năng sinh công của điện trường trong sự di chuyển của điện tích [imath]q[/imath] giữa hai điểm M, N trong điện trường là hiệu điện thế, được xác định: [imath]U=\frac{A_{MN}}{q}[/imath] và trong điện trường đều ta có: [imath]U_{MN}=E.d[/imath]
Xem thêm kiến thức:
Lớp 12: [Chuyên đề] Dao động điều hòa - Bài toán thời gian
Lớp 11: [Chuyên đề] Điện tích điện trường
Lớp 10: [Chuyên đề] ĐỘNG LỰC HỌC CHẤT ĐIỂM và Chuyển động thẳng biến đổi đều
Lớp 9: [Chuyên đề] Điện từ học và [Chuyên đề] Điện học
Nếu bạn là một người học không tốt môn vật lí? Không biết bắt đầu từ đâu? Không biết phân dạng cũng như cần tìm hướng dẫn chi tiết từng phần của môn học này thì đây là topic dành cho bạn! Mình không đảm bảo nó hữu ích với tất cả mọi người nhưng mình sẽ cố gắng trình bày một cách dễ hiểu, xúc tích và cô đọng nhất!
Chuỗi [Chuyên đề] Tổng hợp kiến thức vật lí sẽ diễn ra ở các khối 9,10,11 và 12. Các bạn chú ý theo dõi để đón nhận nhé!
CHUYÊN ĐỀ ĐIỆN TÍCH ĐIỆN TRƯỜNG
PHẦN A: Kiến thức cơ bản lực điện, điện tích trong điện trường
PHẦN B: Một số dạng toán về lực điện, điện tích trong điện trường
- Dạng 1: Bài toán xác định lực tương tác giữa 2 điện tích
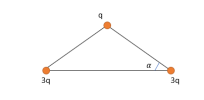
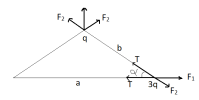
- Dạng 2: Bài toán điện tích chịu tác dụng của nhiều lực, lực tác dụng cân bằng
- Dạng 3: Bài toán lực điện tác dụng lên điện tích trong điện trường
- Dạng 4: Bài toán công của lực điện và chuyển động của điện tích dọc theo đường sức điện trường
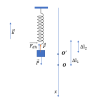
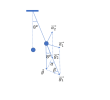
- Dạng 1: Bài toán con lắc chịu tác dụng của lực điện trường
- Dạng 2: Bài toán chuyển động electron quang điện trong điện trường
- Dạng 3: Bài toán chuyển động electron trên quỹ đạo dừng
PHẦN A: Kiến thức cơ bản lực điện, điện tích trong điện trường
I, Lực tương tác giữa hai điện tích (Lực Cu-lông)
- Khi hai điện tích điểm đứng yên đặt gần nhau trong môi trường điện môi đồng chất thì giữa chúng có lực tương tác điện (hay lực tương tác Cu-lông)
- Vecto lực tương tác giữa 2 điện tích đứng yên trong môi trường điện môi đồng tính có đặc điểm:
- Điểm đặt: Tại các điện tích
- Phương: trùng với đường thẳng nối 2 điện tích
- Chiều: Hướng ra ngoài nếu các điện tích cùng dấu (lực đẩy) và hướng vào trong nếu các điện tích trái dấu (lực hút)
- Độ lớn: [imath]F=k.\frac{|q_1q_2|}{\varepsilon r^2}[/imath]
- Xung quanh điện tích có điện trường, điện trường là một dạng vật chất bao quanh các điện tích và gắn liền với điện tích. Điện trường tác dụng lực điện lên điện tích khác đặt trong nó.
- Đại lượng đặc trưng cho độ mạnh yếu của điện trường về phương diện lực tác dụng lực và cường độ điện trường [imath]\vec{E}[/imath] có đặc điểm:
- Điểm đặt: Tại điểm xét cường độ điện trường
- Phương: trùng với phương của lực điện tác dụng lên điện tích thử [imath]q[/imath]
- Chiều: Cùng chiều với lực điện nếu điện tích thử [imath]q[/imath] dương và ngược chiều với chiều lực điện nếu điện tích thử [imath]q[/imath] âm
- Độ lớn: [imath]E=\frac{F}{q}[/imath]
- Lực điện [imath]\vec{F}[/imath] cùng chiều với điện trường [imath]\vec{E}[/imath] khi [imath]q[/imath] là điện tích dương, ngược chiều [imath]\vec{E}[/imath] khi [imath]q[/imath] là điện tích âm.
|||, Công của lực điện trường
- Khi một điện tích [imath]q[/imath] đặt trong điện trường, thì nó sẽ bị lực điện trường di chuyển và sinh công.
- Nếu điện trường đều thì công di chuyển của điện tích là [imath]A=qEd[/imath] với [imath]d[/imath] là hình chiếu của độ dời lên phương đường sức.
- Đại lượng đặc chưng cho khả năng sinh công của điện trường trong sự di chuyển của điện tích [imath]q[/imath] giữa hai điểm M, N trong điện trường là hiệu điện thế, được xác định: [imath]U=\frac{A_{MN}}{q}[/imath] và trong điện trường đều ta có: [imath]U_{MN}=E.d[/imath]
Xem thêm kiến thức:
Lớp 12: [Chuyên đề] Dao động điều hòa - Bài toán thời gian
Lớp 11: [Chuyên đề] Điện tích điện trường
Lớp 10: [Chuyên đề] ĐỘNG LỰC HỌC CHẤT ĐIỂM và Chuyển động thẳng biến đổi đều
Lớp 9: [Chuyên đề] Điện từ học và [Chuyên đề] Điện học