b1: a, chỉ là thay số: trong giây [imath]t_2[/imath]: 6m; sau giây [imath]t_2[/imath]: 8m; b, c, đã được mn giải rồi, đồ thị chỉ là đường parabol [imath]y=2x^2[/imath]Phần này cũng hay mà ít bạn trả lời quá nhỉ ^^
Chị gửi đáp án nè
Mình qua phần này hấp dẫn hơn nè ^^ Mình qua loại 3 nha!
CHUYỂN ĐỘNG THEO QUY LUẬTPhương pháp:
+ Xác định quy luật của chuyển động
+ Tính tổng quãng đường chuyển động. Tổng này thường là tổng của một dãy số
+ Giải phương trình nhận được với số lần thay đổi vận tốc là số nguyên
+ Có thể vẽ đồ thị/đọc đồ thị để tự luận ra quy luật
Lưu ý:
1. Nên so sánh các tổng thời gian/tổng quãng đường với điều kiện cho trước để giới hạn được đáp án chính xác.
2. Không nên tính chung một lần mà nên chia ra nhiều khoảng nhỏ ứng với các quy luật khác nhau, thời điểm khác nhau để tránh sai sót và nhầm lẫn!
Bài tập:
Bài 1: Một viên bi được thả lăn từ đỉnh dốc xuống chân dốc. Bi đi xuống nhanh dần và quãng đường mà bi đi được trong giây thứ i là sk=4k-2 ( k=1;2;....;n), với Sk tính bằng mét (m) và k tính bằng giây (s).
a) Tính quãng đường mà bi đi được trong giây thứ 2; sau 2 giây.
b) Chứng minh rằng quãng đường tổng cộng mà bi đi được sau n giây (k và n là các số tự nhiên) là L(n)=2n^2 (mét)
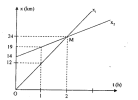
c) Vẽ đồ thị sự phụ thuộc của quãng đường đi được và thời gian chuyển động.
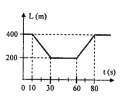
Bài 2: Trên đường thẳng AB dài 81km, xe ô tô đi từ A đến B, cứ sau 15 phút chuyển động thẳng đều, ô tô dừng lại nghỉ 5p. Trong khoảng thời gian 15p đầu, vận tốc của xe thứ nhất là v1=10km/h và trong các khoảng thời kế tiếp, vận tốc của xe lần lượt là 2v1, 3v1, 4v1….Xác định vận tốc trung bình của xe ô tô trên quãng đường AB.
Bài 3: Một động tử xuất phát từ A trên đường thẳng hướng về B với vận tốc ban đầu V0= 1m/s, biết rằng cứ 4s thì động tử ngừng chuyển động trong 2s trong khi chuyển động thì động tử chỉ chuyển động tử chỉ chuyển động thẳng đều. Sau bao lâu động tử đến B biết AB dài 6km?
Tham gia giải @manh huy @Beo'S @nguyenbinhducdat @Chris Master Harry @khanhdiep2k8
b2: quãng đường đi được sau 15*n phút: [imath]S_n = 0,25v_1(1+2+..+n)=1,25n(n+1)[/imath], khi xe đi hết AB thì còn 1 đoạn [imath]\ell[/imath] lẻ ra mà người này đi với vận tốc [imath]v_{n+1}[/imath].
ta tìm đoạn này, xét: [imath]1,25n(n+1)=AB=81[/imath] và lấy n nguyên dương lớn nhất, tức n=7. nói cách khác, người đó đi thêm đoạn [imath]\ell[/imath] với vận tốc [imath]8v_1[/imath] là vừa hết AB. thời gian đi đoạn này: [imath]t_8 = \frac{81-1,25.7.8}{8v_1}=0,1375h[/imath]
=> vận tốc TB: [imath]\bar v = \frac{AB}{(n-1)t'+t_8+nt}[/imath] với t, t' là tgian 15p, 5p nghỉ => [imath]\bar v \approx 33,93km/h[/imath]
b3: sau n*4s thì động tử đến B: [imath]n(4v_0)=AB=6000 => n = 150[/imath] => thời gian cần tìm: [imath]t = 4n+(n-1)2=898s[/imath]
liệu có nhầm lẫn đâu không nhỉ