C
computerscience
Lấy K trên BC sao cho BK=BA
Mà góc ABC=60\Rightarrow Tam giác ABK là tam giác đều.
Do đó:AB=AK(1)
Tam giác ABI là tg vuông cân\Rightarrow AB=AI(2)
Xét tg IAC và tg KAC có:
AC-chung
AI=AK(từ (1) và (2))
KAC=IAC
\Rightarrow tg IAC=tg KAC (c-g-c)
\Rightarrow IAC=KCA=45
Do đó: ICB=90
Xong
Nếu như nhớ không lầm thì cách này giống trong sách nâng cao và phát triển tập 2 (của thầy Vũ Hữu Bình)
Bài này mình còn có cách khác đây :
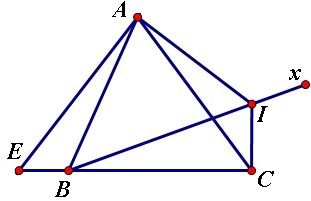
Vẽ [tex]EA \perp AC[/tex]
Ta có : [tex]\widehat{EAB}=\widehat{IAC} (1)[/tex] ( Cùng phụ với [tex]\widehat{BAC}[/tex])
Lại có : [tex]\widehat{IBC}+\widehat{ABI}=\widehat{ABC}[/tex]
[tex]\Leftrightarrow 15^{o}+\widehat{ABF}=60^{o}[/tex]
[tex]\Rightarrow \widehat{ABI}=45^{o}[/tex]
mà [tex] AI\perp AB[/tex] nên [tex]\large\Delta{ABI}[/tex] vuông cân tại A.
[tex]\Rightarrow AB=AI (2)[/tex]
Chứng minh tương tự ta cũng có [tex]\large\Delta{EAC}[/tex] vuông cân tại A
[tex] AE=AC (3)[/tex]
Từ [tex] (1),(2),(3)[/tex] ta suy ra :
[tex]\large\Delta{ABE}=\large\Delta{AIC} (c-g-c)[/tex]
[tex]\Rightarrow\widehat{ICA}=\widehat{BEA}[/tex]
[tex]\Rightarrow \widehat{ICA}=45^{o}[/tex]
Vậy [tex]\widehat{ICB}=90^{o}[/tex]

