H
hiensau99
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
A. Lý thuyết:
I. Các cách tính góc:
1. Sử dụng 2 đường thẳng song song. (đồng vị, so le trong, so le ngoài, trong cùng phí, ngoài cùng phía)
2. Dựa vào định lí tổng 3 góc trong tam giác và hệ quả của định lí này (góc ngoài)
+ Cho 2 góc tính được góc còn lại hoặc góc ngoài không kề với 2 góc đã cho.
+ Cho 2 tam giác có 2 cặp góc bằng nhau thì cặp góc còn lại bằng nhau
3. Đặt vào 2 tam giác bằng nhau.
4. Tính chất đoạn chắn.
5. Sử dụng tam giác cân, tam giác đều
(Các bạn bổ sung thêm nha )
)
II. Hướng giải 1 bài toán tính góc:
1. Vẽ hình chính xác.
2. Đo dự đoán kết quả, định hướng cách làm.
B. Bài tập:
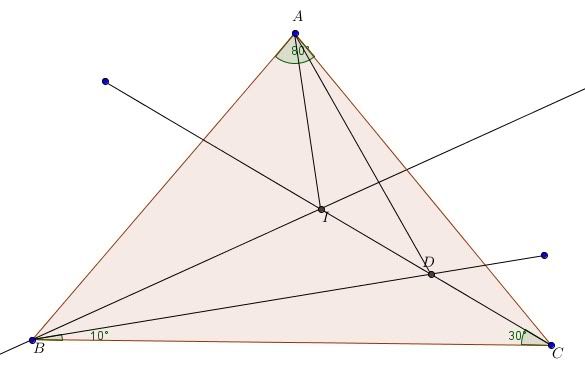
1. Tam giác [TEX]ABC[/TEX] có:[TEX]\hat{B}=45^o ; \hat{C}=120^o[/TEX]. Trên tia đối của tia CB lấy D sao cho CD=2CB. Tính [TEX]\hat{ADB}[/TEX]
I. Các cách tính góc:
1. Sử dụng 2 đường thẳng song song. (đồng vị, so le trong, so le ngoài, trong cùng phí, ngoài cùng phía)
2. Dựa vào định lí tổng 3 góc trong tam giác và hệ quả của định lí này (góc ngoài)
+ Cho 2 góc tính được góc còn lại hoặc góc ngoài không kề với 2 góc đã cho.
+ Cho 2 tam giác có 2 cặp góc bằng nhau thì cặp góc còn lại bằng nhau
3. Đặt vào 2 tam giác bằng nhau.
4. Tính chất đoạn chắn.
5. Sử dụng tam giác cân, tam giác đều
(Các bạn bổ sung thêm nha
II. Hướng giải 1 bài toán tính góc:
1. Vẽ hình chính xác.
2. Đo dự đoán kết quả, định hướng cách làm.
B. Bài tập:
1. Tam giác [TEX]ABC[/TEX] có:[TEX]\hat{B}=45^o ; \hat{C}=120^o[/TEX]. Trên tia đối của tia CB lấy D sao cho CD=2CB. Tính [TEX]\hat{ADB}[/TEX]