M
minhkhac_94
cần gì phải phức tạp hoá thế, cứ áp dụng phương trình lượng giác cơ bản đi mà>-
>-
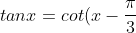\\%20%3C=%3E%20cot(\frac{\pi%20}{2}-x)=cot(x-\frac{\pi}{3})\\%20%3C=%3E%20\frac{\pi%20}{2}-x=x-%20\frac{\pi%20}{3}+k\pi%20\\%20%3C=%3Ex=%20\frac{5\pi%20}{12}+k\pi)
thế thôi là xong
cái này chắc không cần xét điều kiện đâu nhỉ)
=0\\%20%3C=%3E%20sinx=0%20-%20or-%20tan(x-\frac{\pi}{3})=0%20%3C=%3E%20x=%20k\pi%20--%20or--%20x=%20\frac{\pi}{3}+k\pi)
Bài 2
sai vì
A.B=0 <=>A=0 B xác định
hoặc B=0 và A xác định
NÊn vẫn cần ĐK và cần thử lại ĐK
BÀi đầu thử lại ĐK đi herry


